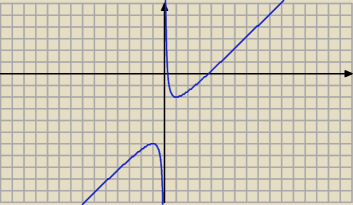
Wykres tej funkcji nie moze byc parabola pomozcie Gracek243: Narysuj wykres funkcji :

	x2−4x+1
f(x)=
	x

adi: to jest parabola ale bez 0 bo nie może w mianowniku być 0.

Gracek243: Nauczycielka mi sprawdzila i powiedziala ze nie moze byc parabola tylko co innego policzylem delte x1 i x2 i wykres narysowalem parabole i zle.. wyszlo mi x²−4x+1 tylko ze x z mianownika co z nim zrobic jak mam to policzyc

Benny: @adi to nie będzie parabola. @Gracek243 miałeś już pochodne? Jeśli tak to przebieg zmienności funkcji i rysujesz.

Mila: x≠0

	1
f(x)=x−4+
	x

Trzeba badać przebieg zmienności funkcji.

Mila: http://www.math.com.pl/analiza-matematyczna-1/badanie-przebiegu-zmiennosci-funkcji/

Gracek243: @Mila mialem pochodne ale nie wiem w jakich punktach mam narysowac ten przebieg na funkcji

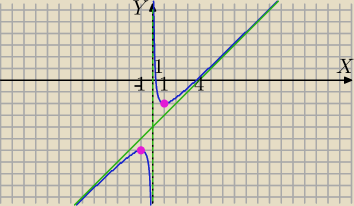
Mila: 1) dziedzina D=R\{0} 2) granice na krańcach dziedziny

	1
limx→−∞(x−4+		)=−∞
	x

	1
limx→0−(x−4+		)=−∞
	x

	1
limx→0+(x−4+		)=∞
	x

	1
limx→∞(x−4+		)=∞
	x

3) ekstrema i monotoniczność.

	1
f'(x)=1−
	x2

f'(x)>0

	1
1−		>0 /*x2 i x≠0
	x2

x²−1>0 (x−1)*(x+1)>0⇔ x<−1 lub x>1 Dla x<−1 oraz dla x>1 funkcja jest rosnąca Dla x∊(−1,0) oraz dla x∊(0,1) funkcja jest malejąca 4) Miejsca zerowe pochodnej ( kandydaci na ekstrema)

	1
f'(x)=0⇔1−		=0
	x2

x=−1 lub x=1 Ponieważ pochodna po przejściu przez te punkty zmienia znak to w x=−1 jest maksimum ( z rosnącej na malejącą)

	1
fmaks=f(−1)(−1)=−1−4+		=−6 [ zaznacz na wykresie punkt (−1,−6) ]
	−1

w x=1 jest minimum f_min=f(1)=−2 [ zaznacz na wykresie punkt (1,−2) ] 5) asymptoty : a) pionowa x=0 (oś Oy) b) ukośne y=ax+b

	x−4+1x		4
a=limx→∞		=limx→∞(1−		+1x2)=1
	x		x

b=lim _x→∞(f(x)−ax⇔

	1
b=lim x→∞(x−4+		−x)=−4
	x

Asymptota ukośna y=x−4 ===============

Gracek243: Juz pomalu kleje o co chodzi dzieki wielkie za pomoc ! pozdrawiam

Mila: