Różniczki Pati: Cześć, wiecie może jak to rozwiązać? Wyznacz wartość najmniejszą i największą funkcji f w podanym przedziale f(x)=x⁴+4³+6 <−2;1>

Janek191: Przepisz jeszcze raz treść zadania f(x) = x⁴ + ...

Pati: f(x)=x⁴+x³+6

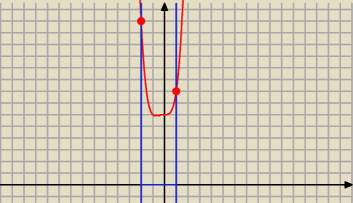
Janek191: f(x) = x⁴ + x³ + 6 Df = < − 2 , 1 >

	3
f '(x) = 4 x3 + 3 x2 = x2*( 4 x + 3) = 0 ⇔ x = 0 lub x = −
	4

f ''(x) = 12 x² + 6 x więc f '' ( 0) = 0 − f ma punkt przegięcia

	3
f ''( −		) > 0 − f ma wtedy minimum lokalne równe
	4

	3		27		229
f( −		) = 6 −		= 5
	4		256		256

Obliczamy jeszcze f( − 2) = 16 − 8 + 6 = 14 f(1) = 1 + 1 + 6 = 8 zatem

	229
ymin = 5
	256

y_max = 14

Pati: Bardzo dziękuję i życzę spokojnego wieczoru.