Rachunek różniczkowy Nilred: Dzień dobry, mam problem z zadaniem: Treść: Wyznacz asymptoty wykresu funkcji f 1)f(x)=¹_x−√x 2)f(x)=√1+x²+x Asymptota pionowa jest wtedy gdy coś nie wchodzi do dziedziny funkcji, a pozioma wtedy gdy licząc lim→∞ lub do −∞ dostanę liczbę. W 1 wyliczyłem, że x=1 jest asymptotą obustronną pionową bo nie wchodzi do dziedziny, czy 0 też jest asymptotą pionową obustronną? Wyszło mi też, że zero jest asymptotą poziomą obustronną. W 2 nie ma asymptot pionowych ani poziomych? Proszę o pomoc, bo nie jestem pewny tych wyników.

Nilred: podbijam

Janek191: z.1

	1
f(x) =		, x > 0
	x − √x

Asymptoty pionowe : x = 0 ( jednostronna) i x = 1 ( obustronna ) Asymptota pozioma jednostronna y = 0

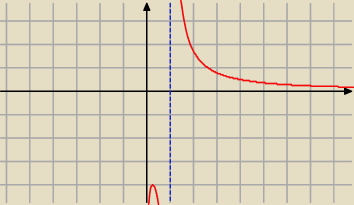
Janek191: lim f(x) = − ∞ x→ 0⁺ lim f(x) = − ∞ x→ 1⁻ lim f(x) = + ∞ x→ 1⁺ lim f(x) = 0 x→+∞

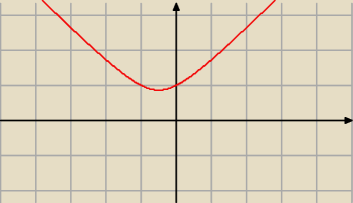
Janek191: z.2 f(x) = √ 1 + x² + x D = ℛ

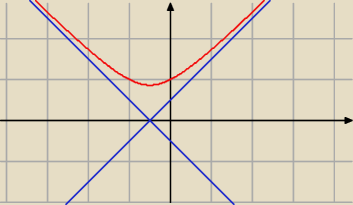
Janek191: Funkcja f(x) = √ 1 + x² + x ma asymptoty ukośne: y = x + 0,5 y = − x − 0,5

Pati: a w 1) jak limx→−∞ to nie równa się także 0? i czemu nie sprawdzamy limx→0− ?

Janek191:

	f(x)
lim		= 1
	x

x→ +∞ lim ( f(x) − x) = 0,5 x →+∞ więc y = x + 0,5 ==========

Pati: Okej, dziękuję za pomoc.

Janek191: Do z. 1 x > 0 D = ( 0 , + ∞ ) bo √x jest określony dla x > 0

Janek191: √x określony dla x ≥ 0 , ale x − √x musi być różne od 0 więc x > 0