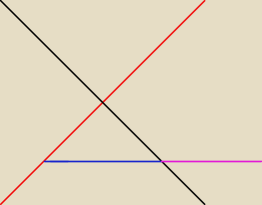
 oblicz objętość bryły ograniczonej powierzchniami x2+z2=9, y2+z2=9, z>=0
Obszar powstały z przecięcia tych walców to kwadrat, po przyrównaniu z wspólna funkcja dla
walców y=x. Czyli mam obliczać dwie całki podwójne po obszarze D, gdzie w 1 przypadku −3<=x<=0
x<=y<=0 i drugi przypadek 0<=x<=3(fiolet) i −x<=y<=0?
problem pojawia się gdy mam obliczyć tą całkę z powierzchni √9−y2dxdy −3<=x<=0(niebieski,
x<=y<=0.
oblicz objętość bryły ograniczonej powierzchniami x2+z2=9, y2+z2=9, z>=0
Obszar powstały z przecięcia tych walców to kwadrat, po przyrównaniu z wspólna funkcja dla
walców y=x. Czyli mam obliczać dwie całki podwójne po obszarze D, gdzie w 1 przypadku −3<=x<=0
x<=y<=0 i drugi przypadek 0<=x<=3(fiolet) i −x<=y<=0?
problem pojawia się gdy mam obliczyć tą całkę z powierzchni √9−y2dxdy −3<=x<=0(niebieski,
x<=y<=0.