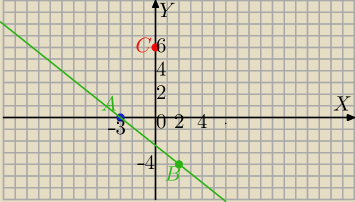
Wyznacz równanie prostej przechodzącej przez 2 punkty. Kuba: Wyznacz równanie prostej przechodzącej przez punkty A(−3;0) i B(2;−4) i sprawdź rachunkowo czy punkty A,B,C (0;6) należą do owej prostej.

Mila: W której jesteś klasie?

Janek191: Takie zadania robiło się w kl. VI podstawówki − około 1980 r.

Kuba: Pytanie nie brzmi w której klasie to robiłeś czy też w której klasie jestem, proszę o rozwiązanie, a nie o stek bzdur

Mila: Pytam, bo są różne metody rozwiązania. I żadnego podtekstu proszę się nie domyślać w moim pytaniu. AB: y=ax+b postać kierunkowa prostej. 0=−3a+b −4=2a+b ========odejmuję stronami 4=−5a

	−4
a=
	5

	−4
0=−3*		+b
	5

	12
0=		+b
	5

	12
b=−
	5

	4		12
y=−		x−
	5		5

C=(0,6)

	4		12		12
y=−		*0−		=−		≠6⇔C∉prostej AB, (co widać z rysunku)
	5		5		5

Eta:

	yB−yA		4
aAB=		= −
	xB−xA		5

	4		−4		12
AB: y= −		(x−xA)+yA ⇒ y=		x−
	5		5		5