2 exo: Napisz równanie okręgu o środku w punkcie o, o współrzędnych (1,2) i r=4.. Oblicz odległość punktu P (2,1) i prostej o równaniu x+2y=4 od okręgu (x−1)² + (y+1)² =9

5-latek: Podaj postac kanoniczna równania okręgu

Janek191: z.1 Wstaw do wzoru; ( x − a)² + ( y − b)² = r²

Janek191: z.2 P = ( 2, 1) x + 2 y = 4 czyli x + 2 y − 4 = 0 Mamy gotowy wzór na odległość punktu P=(x_o, y_o) od prostej o równaniu A x + B y + C = 0

	I A xo + B yo + C I
d =		=
	√ A2 + B2

Podstaw i oblicz

5-latek: Janek zastanawia mnie to od okręgu

Janek191: Zrobić ?

5-latek: Może tu chodzi o wzjajemne polozenie tej prostej względem tego okręgu ?

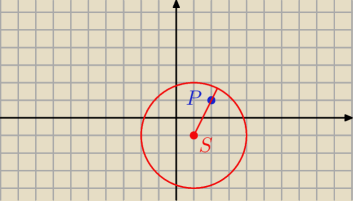
Janek191: P = ( 2 , 1) ( x − 1)² + ( y + 1)² = 3² więc S = ( 1 , − 1) r = 3 Obliczam odległość tego punktu od środka okręgu l PS I = √ ( 1 − 2)² + ( − 1 − 1)² = √ 1 + 4 = √5 Odległość P od okręgu l = I PS I − r = I √5 − 3 I = 3 − √5

Janek191: I część zrobiłem źle , bo miała być odległość prostej od okręgu

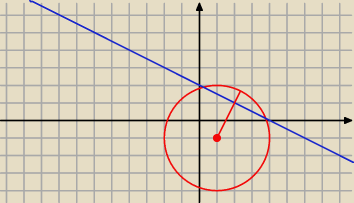
Janek191: x + 2 y = 4 to x + 2 y − 4 = 0 ( x − 1)² + ( y + 1)² = 3² S = ( 1, − 1) r = 3 Mamy l < r l − odległość prostej od środka okręgu.

Janek191: Coś to zadanie mi się nie podoba