Równanie wykładnicze w zadaniu Pb:

	x + 6		1
Dla jakich wartości parametru m (m∊R) równanie |		|=(		)m+5 gdzie x≠3
	x + 3		4

ma więcej rozwiązań ujemnych niż dodatnich?

Janek191: Raczej x ≠ − 3

Pb: Tak, x≠−3, mój błąd

Pb: Czy ktoś ma jakiś pomysł co z tym zrobić?

Eta:

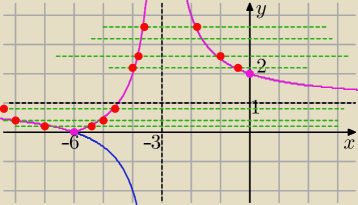
	3
f(x)=1+		, x≠ −3 wykresem jest hiperbola
	x+3

|f(x)| część hiperboli spod osi OX odbijamy nad oś OX ( powstaje różowy wykres proste y=k częściej przecinają wykres po lewej stronie dla k∊<0, 1)U(2, ∞) wtedy dane równanie ma więcej pierwiastków ujemnych niż dodatnich

	1
k= (		)m+5 ∊ <0,1) U (2,∞)
	4

zatem

	1		1
0< (		)m+5 <1 lub (		)m+5>2
	4		4

rozwiąż te nierówności i podaj odp : m∊.....

pr713: k ∊ <0,1> U (2, +∞)***