Wyznacz przedziały monotoniczności funkcji f. Michał:

	4x−5
f(x) =		nie mam pojęcia od czego zacząć...
	x2−1

Janek191: f(x) = U{ 4 x − 5}{ ( x −1)*( x + 1) , x ≠ − 1 i x ≠ 1 Oblicz pochodną tej funkcji ( pochodna ilorazu funkcji )

Michał: No właśnie nie wiem jak obliczyć tą pochodną. liczyłem 3 razy i za każdym razem co innego wyszło. Dało by radę to jakoś dokładniej rozpisać?

Janek191:

	4 x − 5
f(x) =
	x2 − 1

więc

	4*( x2 − 1) − ( 4 x − 5)*2x
f '(x) =		=
	( x2 − 1)2

Eta:

	4(x2−1)−(4x−5)*2x		−4x2+10x−4
f'(x)=		=		.
	(x2−1)2		(x2−1)2

Janek191: f '(x) = 0 ⇔ − 4 x² + 10 x − 4 = 0 oraz rozwiąż nierówności f '(x) < 0 , f ' (x) > 0

Michał: Przepraszam was wszystkich, bo nie byłoby mnie tu gdybym uważał w szkole. Moglibyście poprowadzić to zadanie dalej?

Janek191: − 4 x² + 10 x − 4 = 0 Δ = 100 − 4*(−4)*(−4) = 100 − 64 = 36 √Δ = 6

	− 10 − 6		− 10 + 6
x =		= 2 lub x =		= 0,5
	− 8		− 8

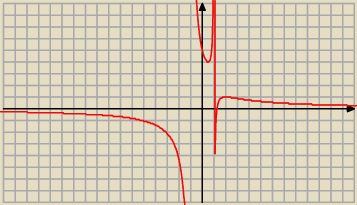
Szkicujemy wykres funkcji g(x) = = − 4 x² + 10 x − 4 Widać, ze dla x ∊ ( 0,5 ; 1 )∪ ( 1, + ∞) jest g(x) > 0 więc wtedy pochodna jest dodatnia czyli funkcja f rośnie. W przedziałach : ( − ∞ , − 1) , ( − 1, 0,5) , ( 2, + ∞ ) − funkcja maleje

Michał: Obliczyłem Δ=10²−4*(−4)*(−4) Δ=100 − 64 Δ=36 √Δ = 6

	−10−6
X1 =		= 2
	2*(−4)

	−10+6		1
X2=		=
	2*(−4)		2

i teraz pewnie muszę rozpoznać jak rozrysować to na wykresie... Dobra jeszcze przypomnijcie mi jak się to rozpoznawało

Michał: A dobra bo ja to mam opóźnienie i jak pisałem to wskoczyło twoje