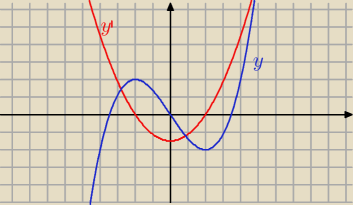
PILNE Zbadaj przebieg zmienności funkcji i naszkicuj jej wykres Cocacola: Proszę o pomoc w rozwiązaniu następującego zadania : Zbadaj przebieg zmienności funkcji i naszkicuj jej wykres. y=(1/8)x³−(3/2)x

Cocacola: Dziedzina to D=R? Punkty przecięcia z OX to (2√3,0) a z OY (0,0) Mógłby mi to ktoś sprawdzić i pomóc z resztą?

Janek191: Tak Teraz oblicz pochodną i jej miejsca zerowe

Cocacola: a jak to zrobić? mógłbyś mim pomóc?

Janek191:

Janek191:

	1		3		3		3
y ' =		* 3 x2 −		=		x2 − 1,5 = 0 ⇔		x2 = 1,5 ⇔ x2 = 4 ⇔
	8		2		8		8

⇔ x = − 2 lub x = 2 Druga pochodna

	3		3
y'' =		*2 x =		x
	8		4

zatem dla x = −2 jest y'' = −1,5 < 0 dlatego funkcja osiąga w punkcie x = − 2 maksimum lokalne równe

	1
ymax =		*(−2)3 − 1,5*(−2) = − 1 + 3 = 2
	8

oraz dla x = 2 jest y'' = 1,5 > 0 dlatego funkcja osiąga w punkcie x = 2 minimum

	1
lokalne równe ymin =		*23 − 1,5*2 = 1 − 3 = − 2
	8

Janek191:

	3
Ponieważ pochodna y' =		x2 − 1,5 jest dodatnia dla x < − 2 więc
	8

dana funkcja rośnie w ( − ∞, − 2) y ' < 0 dla x ∊ ( − 2 , 2) więc dana funkcja maleje w ( − 2, 2) y ' > 0 dla x > 2 więc dana funkcja rośnie w ( 2 , + ∞).

Cocacola: dziękuje! a mogłbys mi jeszcze sprawdzić czy to jest dobrze? funkcja przyjmuje wartosci dodatnie w przedzisle (2√3, +nieskonczonosc) a ujemne (−nieskonczonosc,0) oraz (0,2√3)

Janek191: Masz narysowany wykres funkcji − kolor niebieski, więc źle

Cocacola: a więc jak to obliczyć?

Janek191:

	1		1
y = 0 ⇔		x3 − 1,5 x = 0 ⇔ x*(		x2 − 1,5) = 0 ⇔
	8		8

	1
⇔ x = 0 lub		x2 = 1,5 ⇔ x = 0 lub x2 = 12 = 4*3 ⇔
	8

⇔ x = 0 lub x = − 2√3 lub x = 2√3 − miejsca zerowe więc y > 0 dla x ∊ ( − 2√3 , 0 ) ∪ ( 2√3 , + ∞) y < 0 dla x ∊ ( − ∞, − 2√3 ) ∪ ( 0, 2√3)

Cocacola: a czy druga pochodna ma punkty przegięcia?

Janek191: Nie II pochodna, ale dana funkcja ma punkt przegięcia dla x = 0.

Cocacola: mam takie polecenie: analizując drug pochodną określ przedzialy wklęsłości, wypukłości i ustal ewentualne punkty przegięcia jak to ogarnąc?

Cocacola: i jeszcze prosze o sprawdzenie: y(−x)=−1/8 x³ − 3/2 x= −1/8 x −(−3/2x)=−1/8 x³+3/2 x f nie jest parzysta −y(−x)= −(−1/8x3 +3/2x)=1/8 x³−3/2x funkcja jest nieparzysta

Janek191: Jeżeli II pochodna jest równa 0 , to jest punkt przegięcia.

	3
Dla x = 0 jest y '' =		*0 = 0
	4

−−−−−−−−−−− Dla x < 0 jest y'' < 0 − funkcja jest wklęsła ( − ∞ , 0) − f jest wklęsła ==================== Dla x > 0 jest y '' > 0 − funkcja jest wypukła ( 0 , + ∞ ) − f jest wypukła ==================== Patrz na wykres − kolor niebieski

Janek191: Źle

	1
y = f(x) =		x3 − 1,5 x
	8

więc

	1		1
f( − x) =		(− x)3 − 1,5*( −x) = −		x3 + 1,5 x = − f(x)
	8		8x

Funkcja f jest nieparzysta.

Janek191: To x w mianowniku jest zbędne

Cocacola: dzięki wielkie! mam jeszcze jedną prośbę o obliczenie granicy i asymptot

Cocacola: próbuje i cały czas mi nie wychodzi

Cocacola:

Janek191:

	1		1
y = f(x) =		x3 − 1,5 x = x*(		x2 − 1,5)
	8		8

więc lim f(x) = − ∞ x → −∞ oraz lim f(x) = + ∞ x → +∞

Janek191:

	f(x)		1
lim		= lim		x2 − 1,5 = + ∞
	x		8

x→ −∞ x→ −∞ oraz

	f(x)
lim		= + ∞
	x

x→ +∞ więc brak jest asymptot.

Cocacola: a dlaczego wyszły nieskończoności?

J: bo takie są granice tego trójmianu ( parabola )

Cocacola: czyli nie ma asymptot poziomych, pionowych ani ukośnych?

J: nie ma

Cocacola: a jak zrobić tabelę przebiegu zmienności funkcji?

Cocacola: