Oblicz wysokości trójkąta. kooot: Boki trójkąta wynoszą 8, 12 i 16. Oblicz wysokości trójkąta i promień okręgu wpisanego w ten trójkąt. Mógłby ktoś podpowiedzieć, jak się do tego zabrać..?

kooot: Myślałem, żeby wykorzystać wzór Herona...

Ajtek: No to działaj .

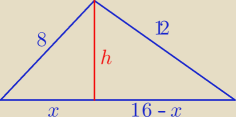
Janek191: Tw. Pitagorasa h² + ( 16 − x)² = 12² h² + x² = 8² −−−−−−−−−− odejmujemy stronami 256 − 32 x = 144 − 64 32 x = 256 − 80 = 176 x = 5,5 =====

	135		9*15
h2 = 82 − x2 = 64 − 30,25 = 33,75 =		=
	4		4

h = 1,5 √15 ==========

Janek191: Teraz oblicz pole Δ oraz r z wzoru

	2 P
r =
	L

L = a + b + c = 36

Janek191:

	2
r =		√15 ≈ 2,58
	3

Franc:

	1
p =		(8 + 12 + 16) = 18, p − 8 = 10, p − 12 = 6, p − 16 = 2,
	2

Pole P = √18 * 10 * 6 * 2 = √9 * 2 * 2 * 5 * 3 * 2 * 2 = 12√15 Wysokości:

	2*12√15		2*12√15		2*12√15		3√15
h1=		=3√15, h2=		=2√15, h3=		=
	8		12		16		2

	12√15		2√15
Promień okręgu wpisanego r =		=
	18		3

kooot: Dzięki wielkie

Janek191: Trzeba było policzyć jedną czy wszystkie wysokości ?

Franc: A jeśli jedną, to którą? Pytanie bez sensu, bo dlaczego ma być uprzywilejowana wyborem jedna z wysokości? Polecenie brzmi: "Oblicz wysokości trójkąta" a nie oblicz wysokość trójkąta

Janek191: Jak mam jedną z wysokości i pole oraz wszystkie boki, to już łatwo policzyć pozostałe wysokości a h_a = b h_b = c h_c