planimetria Eta: Witam wszystkich Widzę,że się nudzicie, to wrzucam zadanka dla chętnych zad1/ W rombie ABCD o boku długości a punkt M dzieli bok rombu w stosunku 2:3 licząc od wierzchołka. Obliczyć pole rombu wiedząc,że odległość punktu M od przekątnej AC jest trzy razy mniejsza od odległości punktu M od przekątnej BD. zad2/W czworokącie wypukłym ABCD o bokach |AB|=a , |DC|=b, |AD|=c , BC|=d w którym c+d=b oraz dwusieczne kątów BCD i ADC przecinają się w punkcie S Wykaż,że |AS|=|BS| Pozdrawiam

kyrtap: Eta lepiej wylicz mi prawdopodobieństwo na ile mam szansę przejść sesję

Eta: Sorrry zapomniałam,że jest

Saizou :

	915
zadanie 1, odpowiedź to P=		a2
	4

Eta:

Saizou : a ten stosunek to od jakiego wierzchołka ?

kyrtap: Eta nie kłam

Kacper: Może jutro A skąd te zadanka?

bezendu: Kacper spojrzysz na mój temat z rachunkiem, przepraszam ze spam.

Eta: Licząc od wierzchołka A

Kacper: Dzisiaj nie myślę, żeby cokolwiek robić

Eta: Kacper .... ja mam czas, ja poczekam

Qulka:

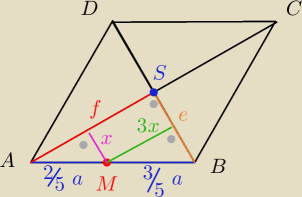Saizou : z podobieństwa trójkątów mamy że

x		e		2		5
	=		→ax=		ae→e=		x
2   a 5		a		5		2

f		3x		3
	=		→3ax=		af→f=3x
a		3   a 5		5

z tw. Pitagorasa mamy że e²+f²=a²

25
	x2+9x2=a2
4

61
	x2=a2
4

	4		2
x2=		a2→x=		a
	61		√61

	1		5		4		60
P=		*2e*2f=2*3x*		x=15x2=15*		a2=		a2
	2		2		61		61

Eta:

	4
Odp: P=		a2
	5

Szukaj błędu

Saizou : bo f=5x

125
	x2=a2
4

	4
x2=		a2
	125

	1		5		4		4
P=		*2e*2f=2ef=2*		x*5x=25x2=25*		a2=		a2
	2		2		125		5

Eta: .......

Kacper: No i nie mam się co wysilać Idę na mecz, bo robi się gorąco

Eta: Kacper zostało jeszcze ..zad 2/

Hugo: Saizo to trzeba robić całkami podwójnymi AMATORSZCZYZNA P = ∫∫dxdx D x₁ ≤ x ≤ x₂ f(x₁) ≤ y ≤ f(x₂)

+-:

Eta: ?

Saizou : Hugo może ta odległość nie była odległością euklidesową

Bogdan: dla +−