ciągi kulkka: utworzono ciąg kolejnych liczb większych od −20, które przy dzieleniu przez 5 dają reszte 2. wyznacz wzór na sumę n początkowych kolejnych wyrazów tego ciągu

Janek191: Te liczby mają być większe od ( − 20), czy od 20 ?

kulkka: (−20)

5-latek: a₁= −18 bo −18=−4*5+2

Janek191: − 18, − 13, − 8, − 3, 2, 7, 12 , 17, 22 , ... a₁ = − 18 r = 5 a_n = a₁ + ( n − 1)*r = − 18 + ( n −1)*5 = − 18 − 5 + 5 n = 5 n − 23 więc S_n = 0,5*(a₁ + a_n)*n = 0,5*( − 18 + 5 n − 23)*n = −20,5 n + 2,5 n² S_n = 2,5 n² − 20,5 n ================

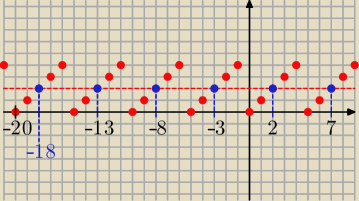
Bogdan: Rysunek pokazuje wykres funkcji, która każdej liczbie całkowitej podzielonej przez 5 przyporządkowuje reszty z tego dzielenia, wartości tej funkcji ∊ {0, 1, 2, 3, 4}. Ciąg arytmetyczny (a_n): a₁ = −18, r = 5, a_n = −18 + 5(n − 1) = 5n − 23 Otrzymaliśmy ciąg liczb: −18, −13, −8, −3, 2, 7, 12, 17, ...