ciag as1409: ile dodatnich wyrazów ma ciąg wyrazony wzorem a_n (5−n)(n−10)/n+3 ?

olekturbo:

	(5−n)(n−10)
an > 0 ⇔		> 0
	n+3

Benny: rozwiąż a_n>0

5-latek: Rozwiaz nierownosc wielomianowa (5−n)(n−10)(n+3)>0

as1409: to wiem, chodzi mi o to jak zapisac rozwiązanie

5-latek: https://matematykaszkolna.pl/strona/142.html

as1409: no dobra, rozwiazania wychodza −3,5,10?

5-latek: Zauwaz ze rozwiązaniem równania sa konkretne liczby Ty masz nierownosc

as1409: no to zbiory beda? przedziały otwarte

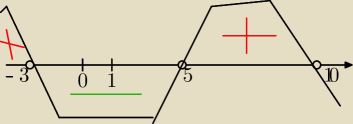
5-latek: Ta nierownosc przyjmuje wartości dodatnie w przedziale n∊(−∞,−3) U(5,10) Wyrazy ciągu naleza n∊N₊ (czyli naleza do liczb naturalnych dodatnich Wiec który przedzial będzie brany pod uwagę czy (−∞,−3) czy (5,10) ?

5-latek: Zauwaz ze piszsemy wyraz ciągu a₁, a₂, a₃ ,a₄ itd. a nie piszsemy wyraz ciągu np. a₋₁₅ a{−10} tak ? Wiec masz już wskazowke który przedzial wybrać