f.cyklometryczne tyu: Witam Próbuję rozwiązać ten http://www.zadania.info/d434/4452847 przykład ale nie wiem, dlaczego prawdziwa jest równość

	− π		− π
arctg(tg(		) =
	8		8

Pomógłby ktoś ?

Mila:

	π		π
arctg(tg(x))=x dla x∊(−		,		)
	2		2

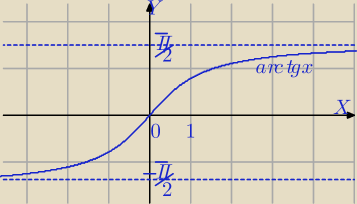
arctgx i tgx są funkcjami odwrotnymi w odpowiednich przedziałach.

7π		π
	>
8		2

	7π		7π
tg(		)=tg(		+k*π), k∊C
	8		8

Dla k=−1 mamy:

	7π		7π		1
tg(		)=tg((		−1*π)=tg(−		π) i
	8		8		8

	π		π		π
−		∊(−		,		)
	8		2		2

W takim razie:

	7π		1		π
arctg(tg(		))=arctg(tg(−		π))=−
	8		8		8

Saizou :

	π		3
Czy możemy zdefiniować arctgy dla y∊(		,		π) ?
	2		2

Saizou : czyli nie brać jego dziedziny naturalnej tylko "dziedzinę przesuniętą"

tyu:

	− π		π
wydaje mi się, że powinniśmy rozpatrywać tylko dla y∊(		,		)
	2		2

Saizou : to była pyt. do Mili, bo chodzi o to że arctgy możemy rozpatrywać w odpowiednich przedziałach, bo to funkcja cyklometryczna, wiec co za różnica czy będziemy brać y∊(−π/2, π/2) czy przesunięte o π

tyu: chyba coś już zaczynam rozumieć. Dziękuję za wytłumaczenie tego przykładu