pomocy tomek: zad 4 wyznacz pole trójkąta prostokątnego , wiedząc że wysokość poprowadzona z wierzchołka kąta prostego podzieliła przeciwprostokątną na dwa odcinki długości 3cm i 4cm zad 5 Przez 15 dni roboczych pewien właściciel sklepu osiedlowego notował dzienny utarg i uzyskał następujące kwoty w złotych : 5200 , 5500 , 4800 , 4800 , 5200 , 5700 , 5700 , 4900 , 4800 , 5000 , 5200 , 5500 , 5200 ,5700 , 5000.Czy mediana dziennego utargu jest niższa od średniej wartości dziennego utargu ? zad 7 rozwiąż równania

	x
a)		=−1
	4x−1

	5		3
b)		−		=0
	2x+1		2x−1

	6		2
c)		−		=1
	x		x−1

tomek: pomocy

tomek: ponawiam prosbe o pomoc te zadania musze zrobic na prace kontrolna tak wiec prosze mi pomoc

tomek: prosze mi tylko podpowiedziec jak mam 1zad i 3 zad obliczyc

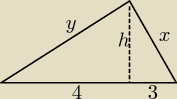
BiebrzaFun : zad4) h²+9=x² h²+16=y² x²+y²=49 h²+9+h²+16=49 2h²=24 h²=12 h=2√3 P=0,5*7*2√3=7√3 zad7) a) zał 4x−1≠0⇒x≠1/4 x=−(4x−1) x=−4x+1 5x=1 x=1/5 b) zał 2x−1≠0 i 2x+1≠0 ⇒x≠1/2 i x≠−1/2

5(2x−1)		3(2x+1)		10x−5−6x−3
	−		=		=0⇔4x−8=0⇒x=2
(2x+1)(2x−1)		(2x+1)(2x−1)		4x2−1

tomek: prosze mi pomoc jeszcze z c) przy zdaniu 7

tomek: prosze mi pomoc jeszcze z c) przy zdaniu 7

rozalia: 6/x − 2/x−1 = 1 Mamy dwa ułamki , pierwszy o mianowniku x, drugi o mianowniku x−1. Należy się od nich uwolnić. Zatem trzeba pomożyć obie strony równania prze mianowniki obu ułamków. Jeżeli pierwszy pomnożymy przez x,to licznik z mianownikiem się uprości i zostanie licznik czyli liczba 6. Ale tę pierwszy ułamek musimy pomnożyć przez mianownik drugiego ułamka czyli x−1 i tu się już nic nie da uprośćić. Najprostsze wytłumaczenie to jest (mnożenie na krzyż) mianownik pierwszego ułamka mnożymy przez licznik drugiego ułamka, natomiast mianownik drugiego ułamka możymy przez licznik pierwszego ułamka. To co jest po prawej stronie mnożymy przez mianowniki dwóch ułamków/ 6/x−2/x−1 = 1 (obie strony mnożymy przez mianowniki x i x−1 6(x−1) − 2*x= 1 * x * (x−1) 6x − 6 − 2x= x(x−1) 6x − 6 − 2x = xkwadrat − x − x kwadrat + 6x − 2x + x − 6 = 0 − xkw + 5x − 6 = 0 z tego trzeba obliczyć deltę, i pierwiastki.