rozwiązać całkę
BlueEDEN:
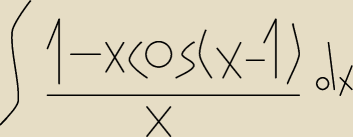
rozwiązać całkę
5 cze 07:02
Janek191:
| | 1 − x*cos ( x − 1) | |
∫ |
| dx = ∫ x−1 dx − ∫ cos (x −1)dx = ... |
| | x | |
x − 1 = t
d x = dt
itd.
5 cze 07:36
BlueEDEN: niestety nie rozumiem tego zbytnio

5 cze 07:45
Janek191:
| | 1 | |
∫ x−1 dx = ∫ |
| dx = ln I x I + C1 |
| | x | |
oraz
podstawienie
x − 1 = t
więc
d x = dt
∫ cos ( x − 1) dx = ∫ cos t dt = sin t + C
2 = sin ( x − 1) + C
2
zatem
| | dx | |
∫ |
| − ∫ cos ( x − 1) dx = ln I x I +C1 − sin( x −1) + C2 = ln I xI − sin (x −1) + C |
| | x | |
5 cze 07:54
BlueEDEN: no to rozumiem ale skąd te ∫ x−1 dx ?
5 cze 07:57
Janek191:
| | 1 | |
Można nie pisać x−1 ale |
| |
| | x | |
| 1 − x*cos (x − 1) | | 1 | |
| = |
| − cos (x − 1) |
| x | | x | |
5 cze 08:07
BlueEDEN: a gdzie się podziało to x przed cosinusem?

skróciło się?
5 cze 08:11
Janek191:
Tak

5 cze 08:11
BlueEDEN: a no to rozumiem, dzięki

5 cze 08:17
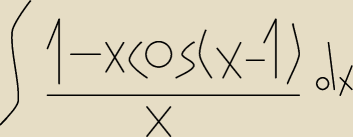 rozwiązać całkę
rozwiązać całkę

 skróciło się?
skróciło się?

