Geometria Analityczna ugabuga: 1) przez punkt A(2,−1,2) poprowadzić płaszczyznę do prostej:

x		y−2		z+1
	=		=
−2		−3		1

2) przez punkt A(2,−1) poprowadzić prostą prostopadłą do prostej:

x		y
	+		=1
6		4

poproszę o jakieś wskazówki jak to rozwiązać

Janek191:

	x		y
2)		+		= 1 / * 12
	6		4

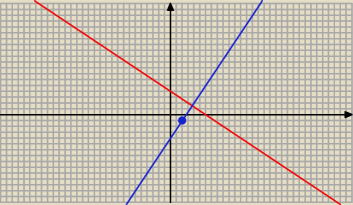
2 x + 3 y = 12 3 y = − 2 x + 12

	2
y = −		x + 4
	3

Prosta prostopadła

	3
y =		x + b i A = ( 2 , − 1)
	2

więc

	3
− 1 =		*2 + b
	2

b = − 4 Odp. y = 1,5 x − 4 ================ W z. 1 popraw treść .

ugabuga: 1) przez punkt A(2,−1,2) poprowadzić płaszczyznę prostopadłą do prostej:

Mila: k^→=[−2,−3,1] wektor kierunkowy danej prostej, k^→ jest prostopadły do szukanej płaszczyzny: Równanie płaszczyzny: π: −2*(x−2)−3*(y+1)+1*(z−2)=0 −2x+4−3y−3+z−2=0 −2x−3y+z−1=0⇔ π: 2x+3y−z+1=0