Rozwiąż nierówności Kamilyoo: a) √x²+7>2x+2 b) 5*√x−3>x+1 Wyniki mają wyjść: a) (−nieskończoność; 1/3) b) (4;19) Proszę o pomoc, bo coś mi nie wychodzi :<

ZKS: Zapisz co Ci nie wychodzi.

Kamilyoo: Np. w pierwszym punkcie podnoszę obustronnie do kwadratu, to co pod pierwiastkiem biorę w wartość bezwzględną i wychodzą 2 przypadki. Jeden ma przedział (−3;1/3) a w drugim delta ujemna

ZKS: Jak podnosisz obustronnie do kwadratu? Przykładowo masz nierówność 1 > −2 / ² 1 > 4 z prawdy dostajesz sprzeczność.

ZKS: Jako, że lewa strona jest nieujemna (pierwiastek parzystego stopnia), to prawa strona również musi być nieujemna, więc należy dać dodatkowe założenie o nieujemności prawej strony.

Kamilyoo: To w takim razie nie wiem jak to zrobić

ZKS: Zrób tak jak napisałem i wtedy podnieś do kwadratu. Zapisz tutaj jak to robisz.

J: Prawa moze byc ujemna

Kamilyoo: Właśnie teraz napisałem to założenie, że 2x+2>0 czyli x>−1, a w odpowiedzi do a przedział idzie od −nieskończoności... Przedział wyszedłby wtedy (−1;1/3)

Kamilyoo: Nie mogłaby być ujemna jakby w drugą stronę znak był

ZKS: J chodziło mi o podniesienie do kwadratu. Teraz zauważ, że jeżeli prawa strona jest ujemna dla pewnych argumentów, które należą do dziedziny to mamy rozwiązanie, ponieważ lewa jako, że jest to pierwiastek stopnia parzystego przyjmuje wartości tylko nieujemne.

Kamilyoo: Sorry, mógłbyś to rozpisać jakoś, bo nie mogę zaczaić?

ZKS: Założenie przed podniesieniem do kwadratu powinno być takie 2x + 2 ≥ 0 (nieujemne). Teraz zrób założenie, że prawa strona jest ujemna i te argumenty muszą należą do dziedziny. Wyjaśnię dlaczego trzeba dać takie założenie. Mamy nierówność √a > b, jeżeli b jest mniejsze od 0 to mamy rozwiązanie, ponieważ jak już pisałem wielokrotnie pierwiastek parzystego stopnia przyjmuje tylko wartości nieujemne, a zatem lewa strona będzie nieujemna natomiast prawa ujemna. Rozumiesz?

J: Jakis chaos , przeciez x = −5 nalezy do rozwiazan, a prawa strona jest ujemna

ZKS: Czytałeś co napisałem J? Jeżeli prawa strona jest ujemna dla pewnych argumentów oraz te argumenty należą do dziedziny, to mamy rozwiązanie z racji tego, że lewa strona jest nieujemna natomiast prawa ujemna.

J: Dlatego wstepne zalozenie o nieujemnosci prawej strony jest nieuzasadnione

ZKS: Zawsze moim zdaniem przed podniesieniem do parzystej potęgi równania czy nierówności należy założyć nieujemność stron. Tak jak pisałem prawdą jest 1 > −2 natomiast 1 > 4 już nie.

Kamilyoo: Dzięki, ZKS. Trochę mi się dzięki Tobie rozjaśniło

ZKS: Na zdrowie. Masz pomysł jak zrobić drugi przykład?

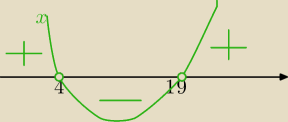
Mila: 5*√x−3>x+1 D: x−3≥0⇔x≥3 Dla x≥3 obie strony nierówności mają wartości nieujemne. 5*√x−3>x+1 /² 25*(x−3)>x²+2x+1 ⇔ 25x−75>x²+2x+1 x²−23x+76<0 i x≥3 Δ=529−304=225

	23−15		23+15
x1=		lub x2=
	2		2

x₁=4 lub x₂=19 x∊(4,19)

pigor: ..., a) √x²+7 > 2x+2 ⇔ ⇔ (√x²+7 > 2x+2 i x∊R i 2x+2< 0) v (√x²+7 > 2x+2 i x∊R i 2x+2 ≥ 0) ⇔ ⇔ (√x²+7 > 2x+2 i x∊R i x< −1) v (√x²+7 > 2x+2 /² i x∊R i x ≥ −1) ⇔ ⇔ x< −1 v x²+7 > (2x+2)² i x ≥ −1) ⇔ ⇔ (*) x∊(−∞;−1) v (x²+7 > 4x²+8x+4 i x ≥ −1) ⇒ 3x²+8x−3 < 0 i (**) x ≥−1 ⇔ ⇔ 3x²+9x−x−3 < 0 ⇔ 3x(x+3)−1(x+3) < 0 ⇔ (x+3)(3x−1) < 0 ⇔ ⇔ 3(x+3)((x−¹₃) < 0 , stąd i z (**) ⇔ −3< x< ¹₃ i x ≥−1 ⇔ −1≤ x< ¹₃ , stąd i z (*) ⇔ x < ¹₃ ⇔ x∊(−∞;¹₃) −−−−−−−−−−−−−−−−−−−−−−−−−−−− b) 5√x−3 > x+1 ⇔ ⇔ (5√x−3 > x+1 i x−3 ≥0 i x+1< 0) v (5√x−3 > x+1 i x−3 ≥0 i x+1 ≥0) ⇔ ⇔ (5√x−3 > x+1 i x ≥3 i x< −1) v (5√x−3 > x+1 /² i x ≥3 i x ≥ −1) ⇔ ⇔ x ∊ ∅ v 25(x−3} > (x+1)² i x ≥3 ⇔ x²−23x+76 < 0 i x ≥3 ⇔ ⇔ 4< x< 19 i x ≥3 ⇔ 4< x< 19 ⇔ x∊(4;19) . ...

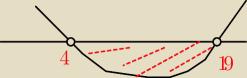
Kamilyoo: Trochę męczył mnie temat tych nierówności i zastanawiałem się czy jest jakaś łatwiejsza opcja rozwiązania tego. Ogarnąłem fajną metodę, więc się nią z Wami podzielę Żadnych dziedzin, kombinowania itp. 5√x−3>x+1 x−3=t² // wprowadzam nową zmienną t x=t²+3 // chyba jasne czyli: 5t>t²+3+1 t²−5t+4<0 (t−1)(t+4)<0 t=1 lub t=4 x−3=1 => x=4 lub x−3=16 => x=19 (parabolka na górze) Temat sprzed kilku dni, ale może komuś się przyda

ZKS: Muszę Cię zmartwić, ale źle rozwiązałeś.

Kamilyoo: Dlaczego źle? Mógłbyś rozwinąć myśl?

5-latek: proponuje Ci wstawić do wyjściowej nierownosci x=4 i x=19

Kamilyoo: Przedział wychodzi dobry x∊(4;19). Tak jak w odpowiedziach. 4 i 19 nie spełniają nierówności i stąd przedział otwarty...

ZKS: Należy tak czy inaczej podać dziedzinę tej nierówności, pomysł z podstawieniem dobry właśnie o taki sposób mi chodziło w pytaniu " Masz pomysł jak zrobić drugi przykład? ". Ustalamy dziedzinę (na sprawdzianach czy maturze zapewne ucięli by Ci punkty za nie ustalenie). 5√x − 3 > x + 1 D = [−3 ; ∞) Następnie robimy podstawienie jak napisałeś t = √x − 3 ⇒ x = t² + 3 i otrzymujemy nierówność postaci 5t > t² + 4 t² − 5t + 4 < 0 t² − t − 4t + 4 < 0 t(t − 1) − 4(t − 1) < 0 (t − 1)(t − 4) < 0 ⇒ t ∊ (1 ; 4) [tutaj masz napisane t + 4 literówka zapewne oraz pod spodem masz zapis jakbyś rozwiązywał równanie, a nie nierówność t = 1 lub t = 4]. Wracamy z początkowym podstawieniem 1 < t < 4 1 < √x − 3 < 4 1 < x − 3 < 16 4 < x < 19 ∧ x ≥ −3 x ∊ (4 ; 19) ∧ x ∊ [−3 ; ∞) ⇒ x ∊ (4 ; 19). Chodziło mi o takie złe rozwiązanie. Wymieniłem wyżej co mi się nie podobało.