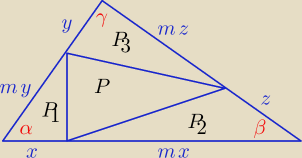
dla chętnych Eta: Zadanie dla chętnych W trójkącie ABC o polu S na bokach AB, AC, BC obrano odpowiednio punkty K, L, M

	|AK|		|CL|		|BM|
tak,że		=		=		=m , m∊R+
	|KB|		|LA|		|MC|

Oblicz pole trójkąta KLM. Pozdrawiam

Godzio: Jutro kolokwium, ale to ciekawsze, może raz wpadnę na jakiś błyskotliwy sposób

Eta:

kyrtap: czyżby podobieństwo?

Eta: Do kogo?

Godzio: Odpowiedź to może

	3m
P = S(1 −		)?
	2(m+1)2

Eta: bez 2 w mianowniku

Eta:

	(m2−m+1)*S
Odp bardziej "elegancka" P=
	(m+1)2

Godzio: Kurczę nie za bardzo wiem gdzie ta dwójka może zniknąć, a błędu nie widzę. S = (m + 1)²xysinα = (m + 1)²xzsinβ = (m + 1)zysinγ

	1
P1 =		mxysinα
	2

	1
P2 =		mxzsinβ
	2

	1
P3 =		myzsinγ
	2

	P1		P2		P3
I teraz dzieląc		,		oraz		otrzymujemy to samo, a stąd
	S		S		S

	m
P1 = P2 = P3 = S *
	2(m + 1)2

	m		3m
P = S − 3 * S *		= S(1 −		)
	2(m + 1)2		2(m + 1)2

Sposób chyba nie za długi, ale na pewno jest jakiś prostszy?

Godzio:

	1
Ale ja głupi jestem S =		...
	2

Więc dwójka znika

Godzio: Eta, mam już temat pracy dyplomowej 'Prawdopodobieństwo ruiny w dwuwymiarowym procesie ryzyka'

Eta:

	1
S=		(m+1)2xysinα
	2

Eta: Widać Godzio,że prawdopodobieństwo Cię nie opuszcza Powodzenia ( i nie doprowadzaj matematyki do "ruiny"

Godzio: Dzięki, oby się nie odbiło jak na maturze Do 1 poszukam jeszcze jakiegoś banalnego sposobu, a później muszę wracać do swoich rzeczy ...

Godzio: Niestety się nie udało, poczekam na mądrzejszych bo jestem ciekaw jak to ugryźć

Kacper: Wieczorem spróbuję