Planimetria Komi: W kole o środku O i promieniu 4 poprowadzono cięciwę AB. Oblicz pola figur na jakie cięciwa podzieliła koło jeśli pole trójkąta AOB jest równe 4√2. Szukałem już rozwiązania na internecie i każde rozwiązanie opierało się na wzorze:

	1
PΔ=		r2*sinα
	2

Mógłby ktoś mi wytłumaczyć łopatologicznie, skąd bierze się ten wzór?

Janek191: To z wzoru na pole Δ P = 0,5 a*b*sin α a = b = r więc P = 0,5 r²*sin α

Komi: A odnosząc się do zadania, czemu jest równy sinα?

Mila: W której klasie jesteś? Czy znasz funkcje trygonometryczne?

Komi: Znam, tylko tu nie ma nigdzie kąta prostego, więc nie umiem sobie wyobrazić czym jest sinα. Już tak się nie denerwuj matematyku...

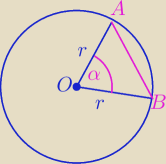
Mila: Ja nie denerwuję się, tylko pytam, aby wytłumaczyć stosownie do Twojej wiedzy. Tu masz wzory na pole trójkąta: https://matematykaszkolna.pl/strona/503.html r=4

	1
Pole obliczymy z wzoru PΔ=		*a*b*sinα, gdzie
	2

α− miara kąta między bokami a i b

	1
PΔAOB=		*4*4*sinα=8sinα
	2

8*sinα=4√2

	4√2		√2
sinα=		=
	8		2

α=45⁰ lub α=135⁰ Dalej poradzisz sobie?

Komi: Zadanie rozumiem . Chcę się po prostu dowiedzieć czemu jest równy w tym zadaniu sinα (który odcinek do którego). Mam rozumieć, że prowadzimy wysokość z punktu A i sinα będzie równy stosunkowi długości tej wysokości do długości promienia r?

Komi: Dobra czaję, dzięki za cierpliwośc i pomoc.