Wyznacz pole trójkąta ABC CHI: Wyznacz pole trójkąta równoramiennego ABC o ramionach AC i BC,w którym podstawa AB jest zawarta w prostej o równaniu y=2x,a dwa wierzchołki mają współrzędne: A=(0,0) C=(−3,4)

Nikka:

	1
P =		|AB|*|CS|
	2

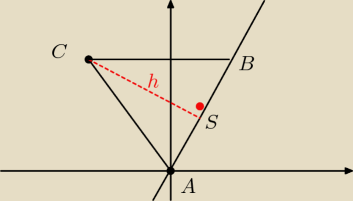
h = |CS| − odległość punktu C od prostej −2x + y = 0 (y = 2x)

	|(−2)(−3)+1*4+0|
h =		→ h = 2√5
	√(−2)2+12

Znajdziemy współrzędne punktu S:

	1
prosta CS: y = ax + b jest prostopadła do prostej y=2x czyli a = −
	2

	1		5
Punkt C należy do prostej CS czyli 4 = −		*(−3) + b → b =
	2		2

	1		5
pr.CS: y = −		x +
	2		2

S∊pr.AB czyli y_S = 2x_S

	1		5
S∊pr.CS czyli yS = −		xS +
	2		2

Stąd x_S = 1, y_S = 2 czyli S = (1,2). Ponieważ trójkąt jest równoramienny to punkt S jest środkiem odcinka AB (podstawy trójkąta) czyli

	xA+xB		yA+yB
xS =		i yS =		(1)
	2		2

Z (1) obliczamy współrzędne punktu B (współrzędne punktów A i S znamy): x_B = 2 i y_B = 4 Obliczamy długość podstawy (odcinka AB): |AB| = √(x_B−x_A)² + (y_B−y_A)²) |AB| = 2√5

	1
P =		*2√5*2√5 = 10
	2