Rozwiąż równania stefan: Rozwiąż równania: a) ctg⁴ x − 2ctg² x − 3 = 0 b) 2sin³ x − 3sin x cos x = 0 c) 4sin³ x − 8sin² x + 2 = 0 d) 4sin(pi*x) = 4x² − 4x + 5

Misyogi: Proszę o rozwiązanie tych równań: a) ctg4 x − 2ctg2 x − 3 = 0 b) 2sin3 x − 3sin x cos x = 0 c) 4sin3 x − 8sin2 x + 2 = 0 d) 4sin(pi*x) = 4x2 − 4x + 5

PW: Cierpliwości, drodzy moi. Na pewno znajdzie się ktoś, co odwali za Was pracę domową, i nawet domyśli się gdzie popełniliście błędy przepisując zadania.

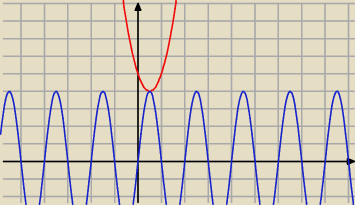
Ada: a) stosując podstawienie ctg²x = t doprowadzamy do równania kwadratowego b) sinx ( 2sin²x − 3cosx) = sinx ( 2[1−cos²x] − 3cosx) sinx = 0 lub −2cos²x−3cosx+2 = 0 c) http://www.wolframalpha.com/input/?i=4sin%5E3x+-+8sin%5E2x+%2B2+%3D+0 wolfram mówi, że to ma brzydkie rozwiązania da się rozwiązać sprowadzając do wielomianu trzeciego stopnia, a te wszystkie się analitycznie rozwiązuje. d) f(x) = 4sinπ(πx)

	1
maksimum → 4 dla x =
	2

g(x) = 4x² − 4x+5

	−b		1		1		1
minimum → p =		=		q = g(p) = 4		− 4		+ 5 = 4
	2a		2		4		2

	1
czyli x =		jedynym rozwiązaniem.
	2

Misyogi: Dzięki

Eta: