Zaznacz na osi liczbowej zbiór rozwiązań nierówności NycU: proszę o pomoc :

	x−3		x−1
a)		< lub =
	x−4		x−3

	4−2x		1−x
c)		>
	x+1		x

	x+3		5−x
d)		<
	1−x		x+2

	4−x		x−3
e)		> lub =
	2x−2		1−2x

	2x+2
f) {4x+2}{2x−6} < lub =
	2x+3

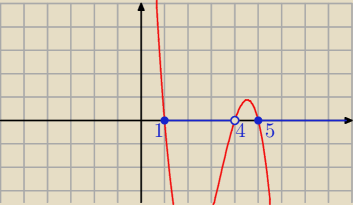Janek191: Np. a)

x − 3		x −1
	≤		, x ≠ 3 i x ≠ 4
x − 4		x − 3

x − 3		x −1
	−		≤ 0, sprowadzamy do wspólnego mianownika
x − 4		x − 3

( x −3)*(x −3) − ( x − 4)*(x − 1)
	≤ 0
( x − 4)*( x − 3)

x2 − 6 x + 9 − ( x2 − x − 4 x + 4)
	≤ 0
( x − 4)*( x − 1)

− x + 5
	≤ 0
( x − 4)*( x − 1)

Można zapisać ( 5 − x)*( x − 4)*( x − 1) ≤ 0 i naszkicować wykres x₁ = 1 , x₂ = 4 , x₃ = 5 Odczytujemy rozwiązanie: <1, 4 ) ∪ < 5, + ∞ ) \ { 3} lub ( 1 , 3)∪ (3,4) ∪ < 5, +∞ ) =============== ====================