6 punktów misio: Czy istnieje na płaszczyźnie 6 punktów, z których każde trzy są wierzchołkami trójkąta równoramiennego.

PW: Spróbuj konstrukcji "w tył". Mając dwa punkty rozstrzygnąć gdzie leży trzeci, dla którego warunek zadania jest spełniony (trzy punkty są wierzchołkami trójkąta równoramiennego). Mając trzy − ustalić, gdzie musiałby leżeć czwarty, dla którego warunek zadania jest spełniony (cztery punkty, każde trzy są wierzchołkami trójkąta równoramiennego). I tak dalej ...

misio: Trzeci punkt musi leżeć na symetralnej, ale przy czterech to nie wiem gdzie musi leżeć ten czwarty

PW: Też na symetralnych, tyle że wszystkich trzech odcinków, które go nie zawierają. Musi być więc środkiem okręgu ...

misio: czyli dla pięciu jak będzie , bo jakoś sobie tego nie mogę wyobrazić

PW: No to piszesz: "Widzę możliwą konstrukcję dla 4 punktów". Dla pięciu punktów^*) a) spełnienie warunków zadania jest niemożliwe, bo ... b) nie widzę dalszej możliwości konstrukcji, która być może istnieje. _______________________________ ^*) Niepotrzebne skreślić.

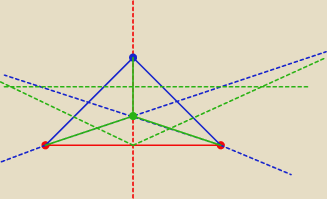
Ada: Jak w takim razie (tak teoretycznie tylko pytam) udowadnia się, że takich konstrukcji zrobić się nie da Bo rysunek to raczej żaden dowód.