Ciągi + logarytm Revio: Zad 1

	n+2
Dany jest ciąg o wyrazie ogólnym an =
	n+3

a) Korzystając z definicji, zbadaj czy ciąg jest arytmetyczny b) Określ monotoniczność tego ciągu Zacząłem liczyć, policzyłem n+1 , później odjąłem ale coś mi nie wychodzi bo w mianowniku zostaje równanie kwadratowe. Pomoże ktoś? zad2

	56 4√5
log5√5		−−> to 5√5 jest całe w indeksie dolnym, tylko tak dziwnie to
	1253

widać.

J: 1) jeśli mianownik ma warość zależną od n , to ciąg nie jest arytmetyczny

Revio: Dzięki Wyszło mi

	1
an+1 − an =
	n2+7n+12

J:

	2		56*51/4
2) =		log5		= ... i licz dalej ..
	3		59

Revio: A do tego logarytmu nie mam pojęcia jak się zabrać

J: no to wyszło Ci,że nie jest arytmetyczny ...

Revio: A jak określić monotoniczność?

J: ustal jakie wartości przyjmuje mianownik, dla n ≥ 1

Revio: Mógłbyś mi podpowiedzieć w jaki sposób to zrobić? Bo dużo mi to nie mówi

J: naszkicuj wykres: y = x² + 7x + 12 i zobacz, jakie wartości przyjmuje dla x ≥ 1 (dodatnie, ujemne, i takie i takie )

Revio: Naszkicowałem, określiłem p i q co mam dalej zrobić?

J: odpowiedz na pytanie, jakie wartości przyjmuje ten trómmian dla x ≥ 1 ?

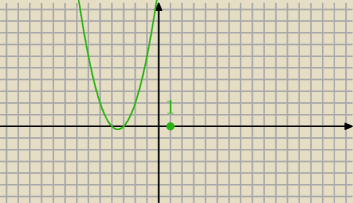
J: Dla n ≥ 1 trójmian przyjmuje wartości dodatnie, a więc: a_n+1 − a_n > 0 , czyli ciąg jest rosnący

Revio: Ok, ogarnąłem, dzięki za pomoc. Problem mam nadal z tym logarytmem , wychodzą mi jakieś dziwne liczby nie wiem jak to zrobić

J:

	1
1) możesz napisac krótko, dla każdego n wyrażenie:		> 0
	n2 + 7n + 12

	2		2		11		11
2) =		log55−11/4 =		*(−		)log55 = −
	3		3		4		3

J:

	11
sorry ... = −
	6

Revio:

	2
Jak pozbyłeś się tego 5√5 przy logarytmie, i skąd wzięło się to		?
	3