pytanue ind: dlaczego jak liczy się maksymalne pole to zawsze szuka się p a nie q

J: a kto Ci to powiedział ?

ind: a kiedy się szuka p a kiedy q jak mam znaleźć max pole a funkcja Mi wyszła −6x²+36x

J: dziecko ..Ty sam/a nie wiesz, o co pytasz .. jakie pole , czego pole ?

ind: czemu od razu dziecko ? jeżeli mam znaleźć maksymalne pole w zadaniu i wychodzi mi funkcja to mam szukać p czy q

J: chyba już wiem , o co Ci chodzi .. rozumiem,że nie znasz pochodnych , zatem rysujesz wykres funkcji: f(x) = −6x² + 36 osiaga ona wartośc maksymalną dla x = x_w = p (odcięta wierzchołka paraboli )

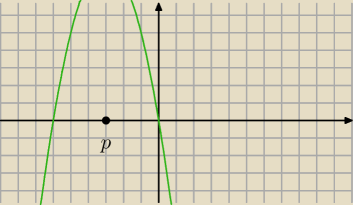
J: maksimum dla x = p

PW: Odpowiedź na postawione pytanie brzmi więc: − Szuka się p, żeby wyliczyć q, o które pytali. Można od razy liczyć q, jeżeli interesuje nas tylko jakie jest największe pole, a nie interesuje dla jakiej wartości x jest ono osiągane. Jest to jednak ryzykowne, w takich zadaniach liczba x ma ograniczone wartości, co wynika z treści zadania (tu nie wiem, bo tej treści nie podałaś). Może się tak zdarzyć, że − mimo iż wzór formalnie określa funkcję kwadratową − dla x należących do dziedziny f_max ≠ f(p) (mówiąc po chłopsku: iksowa współrzędna wierzchołka nie musi należeć do dziedziny, wtedy f osiaga maksimum na jednym z krańców dziedziny). Dlatego nie liczymy od razu q, ale najpierw p − i sprawdzamy, czy p należy do dziedziny. Morał: nigdy nie mówimy o maksimum czy minimum funkcji bez podania dziedziny (sam wzór nie wystarczy).