Planimetria

Planimetria Przemysław: Proszę o sprawdzenie, czy taki dowód jest ok. Zadanie: "Każda z przekątnych czworokąta wypukłego dzieli go na trójkąty o równych polach. Wykaż, że ten czworokąt jest równoległobokiem." Dowód: Warunki zadania spełnia kwadrat. Jest on równoległobokiem. Dowolny czworokąt jest obrazem kwadratu w danym przekształceniu afinicznym. Więc ten czworokąt jest równoległobokiem.

2 cze 00:52

Przemysław: "Dowolny czworokąt wypukły jest obrazem kwadratu w danym przekształceniu afinicznym."

2 cze 00:55

Przemysław:

2 cze 08:56

Przemysław:

2 cze 10:16

Przemysław:

2 cze 12:50

Kacper: A teraz uzasadnij, że dowolny czworokąt wypukly jest obrazem kwadratu w danym przekształceniu afinicznym... emotka

2 cze 13:08

PW: "w danym przekształceniu" to nie dowód, ale pobożne życzenie. Trzeba to przekształcenie zdefiniować.

2 cze 13:09

Przemysław: Hmm... Myślałem, że to zadziała na takiej zasadzie, jak to, że elipsę można przekształcić w dowolną inna elipsę

2 cze 13:14

PW: A w ogóle teza jest fałszywa ... weź coś co nie jest trapezem − ma dwa boki nierównoległe − dlaczego przekątne miałyby dzielić to na trójkąty o równych polach? Podstawy są jednakowe, a wysokości − nie.

2 cze 13:56

PW: Oj, mówię nie na temat. W założeniu jest założenie, że przekątne dzielą czworokąt na trójkąty o równych polach. Moja uwaga z 13:56 nieaktualna.

2 cze 13:58

Przemysław: Hmm... Jest twierdzenie, że trzy dowolne punkty można przekształcić w trzy dowolne. W czworokącie mamy cztery punkty. Więc można najpierw dokonać takiego przekształcenia, że trzy punkty będą tworzyły trójkąt prostokątny równoramienny. Następnie przekształcić 2 punkty (te z przeciwprostokątnej) i jeden punkt (ten który poprzednio zostawiliśmy bez zmian) tak by uzyskać drugi trójkąt, przystający do pierwszego. I tak byśmy mieli kwadrat. A co do 13:09 to chyba nie musimy wiedzieć, jakie dokładnie to przekształcenie, bo chyba wystarczy wiedza, że ono istnieje i jest afiniczne. Oczywiście jest duża szansa, że się mylę

2 cze 14:25

PW: Coś mi jeszcze nie pasuje. Przekształcić trzy w trójkąt prostokątny − zgoda. I mówisz dalej: "następnie przekształcić 2 poprzednie i trzeci" by uzyskać drugi trójkąt prostokątny. Skąd wiadomo, że to drugie przekształcenie jest tym samym co pierwsze?

2 cze 17:32

Eta:

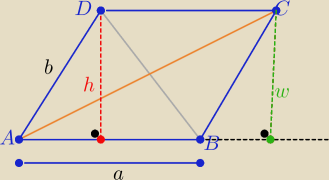
P −− pole czworokąta ABCD

	1
z założenia : P(ΔABD)= P(ΔADC)=P(ΔABC)= P(ΔDBC)=		P
	2

Należy wykazać ,że czworokąt jest równoległobokiem, czyli boki przeciwległe są równoległe P(ABD)= P(ABC) ⇒ a*h= a*w ⇒ h=w ⇒ AB∥DC analogicznie dla trójkątów ACD i ABD ( zaznacz wysokości opuszczone na bok |AD|=b P(ACD)= P(ABD) ⇒ h₁*b= w₁*b ⇒ h₁=w₁ ⇒ AD∥BC zatem: taki czworokąt spełniajacy warunki zadania jest równoległobokiem c.n.w

2 cze 19:06

Eta: Tu masz jeszcze inny dowód: http://www.nowik.com.pl/upload/24/rozw_udowodnij.pdf str. 29 zad. 7

2 cze 20:29

Przemysław: Dziękuję Eta

PW, Ale ich złożenie też będzie przekształceniem?

2 cze 21:24