tryga - Pomocy !!!!!! heban: Cześć Mam do roziwazania 4 zadania. Proszę o pomoc. zad.1 Wyznacz wartości parametru a, a∊ℛ, dla których równanie (cos x − ^√2₂ )( sin x− a )=0 ma trzy różne roziwązania w przedziale <0, 2π> zad.2 Wyznacz wartości parametru k, k∊ℛ, dla których równanie (sinx + ¹₂ )(cos x+ 2k)=0 ma cztery różne rozwiazania w przedziale <−π,π>. zad.3 Wyznacz wartości parametru k, k∊ℛ, dla których równanie (sinx − cos x)(sin x + 0,5k )= 0 ma cztery różne rozwiazania w przedziale <0, ^3π₂ > zad.4 Wyznacz wartości parametru m, m∊ℛ, dla których równanie (2cos x−1)(sin x −m)=0 ma cztery różne rozwiązania w przedziale < − ^π₂ , ^3π₂ > z których trzy są dodatnie.

Przemysław: 1.

	√2
cosx=
	2

ma dwa różne rozwiązania. Ma być jeszcze jedno rozwiązanie, czyli sinx=a ma mieć jedno rozwiązanie na zadanym przedziale czyli a=1 lub a=−1 (każdą z tych wartości sinus przyjmuje tylko raz na tym przedziale) Myślę, że jakoś tak trzeba kombinować po kolei

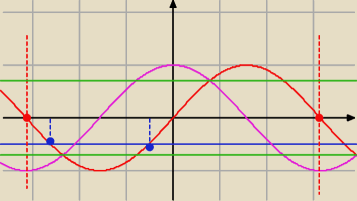Janek191: z.2 ( sin x + 0,5)*( cos x + 2 k) = 0 < − π ; π > sin x + 0,5 = 0 lub cos x + 2 k = 0 sin x = − 0,5 lub cos x = − 2k Równanie sin x = − 0,5 ma 2 rozwiązania w podanym przedziale Aby drugie równanie miało 2 rozwiązania musi zachodzić − 1 ≤ − 2 k < 1 / : ( − 2 ) 0,5 ≥ k > − 0,5 Odp. −0,5 < k ≤ 0,5 ================