

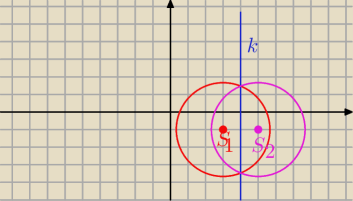
 a) k : x − 4 = 0
( x − 3)2 + ( y + 1)2 = 7
S1 = ( 3, − 1) r = √7
więc
S2 = ( 5, − 1) r = √7
Odp.
( x − 5)2 + ( y + 1)2 = 7
==================
a) k : x − 4 = 0
( x − 3)2 + ( y + 1)2 = 7
S1 = ( 3, − 1) r = √7
więc
S2 = ( 5, − 1) r = √7
Odp.
( x − 5)2 + ( y + 1)2 = 7
==================
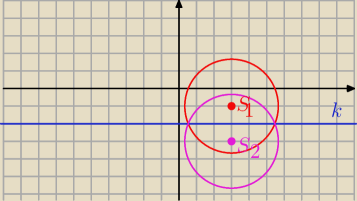 b) k : y + 2 = 0 y = − 2
( x − 3)2 + ( y + 1)2 = 7
S1 = ( 3, − 1) r = √7
więc
S2 = ( 3 , − 3) r = √7
Odp.
( x − 3)2 + ( y + 3)2 = 7
==================
b) k : y + 2 = 0 y = − 2
( x − 3)2 + ( y + 1)2 = 7
S1 = ( 3, − 1) r = √7
więc
S2 = ( 3 , − 3) r = √7
Odp.
( x − 3)2 + ( y + 3)2 = 7
==================
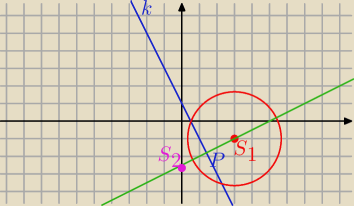 c) k : 2 x + y − 1 = 0 y = − 2x + 1
S1 = ( 3 , − 1)
Prosta prostopadła do k
y = 0,5 x + b ma przechodzić przez S1 = ( 3 , − 1), więc
− 1 =0,5*3 + b
b = − 2,5
y = 0,5 x − 2,5
===========
S2 leży na tej prostej
więc S2 = ( x, 0,5 x − 2,5)
Szukamy punktu wspólnego tych prostych:
− 2 x + 1 = 0,5 x − 2,5 / * 2
− 4 x + 2 = x − 5
− 5 x = − 7
c) k : 2 x + y − 1 = 0 y = − 2x + 1
S1 = ( 3 , − 1)
Prosta prostopadła do k
y = 0,5 x + b ma przechodzić przez S1 = ( 3 , − 1), więc
− 1 =0,5*3 + b
b = − 2,5
y = 0,5 x − 2,5
===========
S2 leży na tej prostej
więc S2 = ( x, 0,5 x − 2,5)
Szukamy punktu wspólnego tych prostych:
− 2 x + 1 = 0,5 x − 2,5 / * 2
− 4 x + 2 = x − 5
− 5 x = − 7
| 7 | ||
x = | ||
| 5 |
| 7 | 5 | 9 | ||||
y = −2* | + | = − | ||||
| 5 | 5 | 5 |
| 7 | −9 | |||
P = ( | , | ) | ||
| 5 | 5 |
| 7 | 7 | ||
− x = 3 − | |||
| 5 | 5 |
| 14 | |
= x + 3 | |
| 5 |
| 1 | ||
x = − | ||
| 5 |
| 1 | 1 | 5 | 1 | 25 | 26 | |||||||
y = | *(− | ) − | = − | − | = − | |||||||
| 2 | 5 | 2 | 10 | 10 | 10 |
| 1 | 26 | |||
S2 = ( − | , − | ) | ||
| 5 | 10 |
| 1 | 26 | |||
( x + | )2 + ( y + | )2 = 7 | ||
| 5 | 5 |