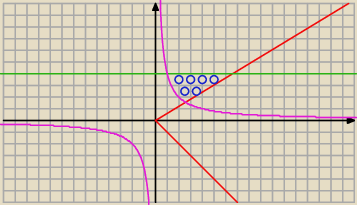
Całka podwójna Dawid: Oblicz całkę

	1
∫ ∫		dxdy D:xy=4 x=|y| y=4
	y

D Nasz obszar całkowania to jest to co zamalowane kółkami zatem jak opisać taki obszar? Dziękuje za pomoc

Kacper: Można podzielić na dwa obszary normalne względem osi OX lub jeden obszar normalny względem osi OY.

Dawid:

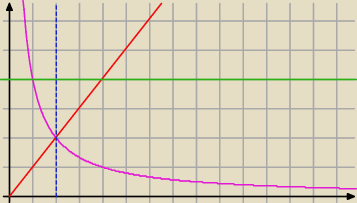
	⎧	1<=x<=2
D1 =	⎨
	⎩	4x<=y<=4

	⎧	2<=x<=3
D2 =	⎨
	⎩	x<=y<=4

Dobrze?

Dawid: Czy inaczej ?

Dawid: czy zamiast x ma być √x²?

Kacper: W drugim dlaczego 2≤x≤3? \√x²=x, dla x≥0

ZKS: Łatwiej przecież jest jak pisał Kacper.

	⎧	2 ≤ y ≤ 4
D =	⎨
	⎩	4y ≤ x ≤ y

Dawid: od 2 do 4 ?

ZKS: Spójrz na rysunek to zobaczysz.

Kacper: Tak, tylko prościej jest robić względem osi OY Aczkolwiek obie metody