 Oblicz całkę podwójną, a więc staram się to zrobić i mógłby mi ktoś powiedzieć co dalej w
pewnym etapie.
∫∫(y+1)dxdy gdy:
D x+y=1
y−x=1
y=2
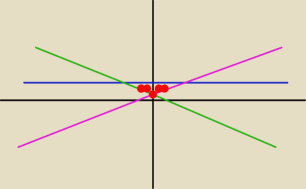
Wykres zrobiłem, ale tutaj taki bardziej prowizoryczny
niebieski : y=2
zielony: y=1−x
różowy: y=1+x
Dalej wyznaczyłem pole ograniczone z dołu i z góry
D: { 1<< y <<2
{ 1−y << x <<−1+y
Następnie zapisałem
2 x=−1+y
∫∫ (y+1)dxdy = ∫ dy ∫ (y+1) dx = ........ i teraz tutaj co muszę zrobić, mógłby mi ktoś
prostym zrozumiałym językiem wytłumaczyć?
D 1 x=1−y
Oblicz całkę podwójną, a więc staram się to zrobić i mógłby mi ktoś powiedzieć co dalej w
pewnym etapie.
∫∫(y+1)dxdy gdy:
D x+y=1
y−x=1
y=2
Wykres zrobiłem, ale tutaj taki bardziej prowizoryczny
niebieski : y=2
zielony: y=1−x
różowy: y=1+x
Dalej wyznaczyłem pole ograniczone z dołu i z góry
D: { 1<< y <<2
{ 1−y << x <<−1+y
Następnie zapisałem
2 x=−1+y
∫∫ (y+1)dxdy = ∫ dy ∫ (y+1) dx = ........ i teraz tutaj co muszę zrobić, mógłby mi ktoś
prostym zrozumiałym językiem wytłumaczyć?
D 1 x=1−y
| 14 | ||
mnie wychodzi | ||
| 3 |