Obliczyć ekstremum. Andrzej: Witam! Obliczyć ekstremum dla: x²−2x+1/x²−4 Próbowałem na kalkulatorze, ale druga pochodna wyszła duża, a minimum i maksimum lokalne są dodatnie: 34/27 i 72/1728. Z góry dzięki, pozdrawiam serdecznie

J: To odpowiedzi masz chyba do innego zadania....

	2(x−1)(x−4)
f'(x) =
	(x2 − 4)2

	3
i ekstrema lokalne: x = 1 (fmax = 0) , x = 4 (fmin =		)
	4

Janek191:

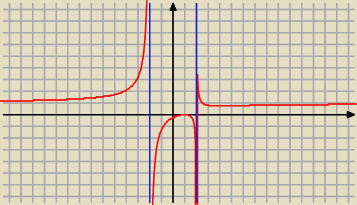
	x2 − 2 x + 1
f(x) =		, x ≠ − 2 i x ≠ 2
	x2 − 4

więc

	( 2 x − 2)*( x2 − 4) − ( x2 − 2 x + 1)* 2 x
f '(x) =		=
	( x2 − 4)2

	2 x3 − 8 x − 2 x2 + 8 − 2 x3 + 4 x2 − 2 x
=		=
	( x2 − 4)2

	2 x2 − 10 x + 8		2*( x2 − 5 x + 4)
=		=		=
	( x2 − 4)2		(x2 − 4)2

	2*( x − 4)*( x − 1)
=		= 0 ⇔ x = 1 lub x = 4
	( x2 − 4)2

	3
fmax = f(1) = 0 oraz fmin = f(4) =
	4

Andrzej: Te dziwne rozwiązania miałem, bo stosowałem się do procedur, których mnie nauczono na studiach: czyli: pierwsza pochodna, jej miejsca zerowe, druga pochodna, zbadanie znaku drugiej pochodnej w każdym punkcie x₀ (gdy druga pochodna jest wyższa od 0) to funkcja ma miminum lokalne jeśli odwrotnie maksimum lokalne i właśnie obliczenie ekstremum i w pierwszym poście zapomniałem dodać, że miałem takie rozwiązania.

J: a kto Ci każe liczyc drugą pochodną ... badasz tylko czy pierwsza zmienia znak ...

Andrzej: Dziękuje że pomogliście

Bogdan: To coraz częściej spotykana postawa. Czekamy, aż nas nauczą, a nie uczymy się sami. Oczekiwanie na podanie wzoru, procedury, szablonu, przepisu, a przez to nie mamy umiejętności i woli samodzielnego studiowania problemu. Bez obrazy Andrzeju, przedstawiłem zjawisko wykorzystując Twoje szczere wyznanie o stosowaniu poznanych procedur. Widać to nawet po sposobie zapisu zadania. Nie chciało się poszukać na forum opisu sposobów zapisywania wyrażeń matematycznych i chyba nie otrzymałeś wcześniej informacji o stosowaniu nawiasów i Twój zapis przyjął niewłaściwą

	1
postać: x2 − 2x +		− 4, a powinien tak wyglądać:
	x2

f(x) = (x² − 2x + 1)/(x² − 4) albo f(x) = (x − 1)²/(x² − 4),

	(x − 1)2
a najlepiej tak: f(x) =		.
	(x2 − 4)