Obliczyć całkę podwójną po prostokącie
CŁK: Proszę o pomoc w rozwiązaniu
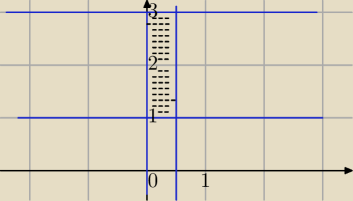
∬sin2πxdxdy G={ 0≤x≤0,5, 1≤y≤3}
G
31 maj 18:52
Mila:
0∫
0.5[
1∫
3(sin(2πx)dy]dx= dalej poradzisz sobie?
31 maj 22:02
CŁK: Niestety nie. Nie wiem jak policzyc ∫sin2πxdy ?
1 cze 10:21
J:
traktujesz: sin2πx jako stałą .... ∫sin2πxdy = sin2πx*y
1 cze 10:24
Marcin Kowalski: A jeśli liczyć to po dx?
1 cze 10:43
J:
| | 1 | |
tutaj masz liczyć po dy .... ale jeśli chcesz wiedzieć po dx: ∫sin2πxdx = − |
| cos2πx + C |
| | 2π | |
1 cze 10:45
Marcin Kowalski: Najpierw chyba liczymy po dy, następnie dx. Chociaż tutaj chyba obojętna jest kolejność, jesli
w
granicach mamy same liczby?
1 cze 10:52
J:
tak ... w tym zadaniu koleność całkowania nie jest istotna
1 cze 10:56
Marcin Kowalski: Ok super, dziękuję
1 cze 11:04