Obliczyć całkę podwójną po obszarze D Norbert: Obliczyć całkę podwójną po obszarze: ∫∫ sin(x+y)dxdy, gdzie D jest obszarem ograniczonym liniam y=0, y=x, x+y=π/2 D Narysowałem wszystkie linie na osi współrzędnych i dalej nie wiem co zrobić bo funkcji sinusa nie można rozbić na 2 całki pojedyncze. Z góry dziękuję

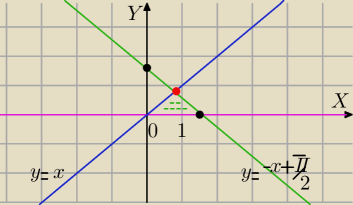
Mila: y=x, x+y=π/2

	π
x+x=
	2

	π
x=
	4

Rozbijasz na dwie całki: ₀∫^π₄[₀∫^xsin(x+y)dy]dx=_^π40∫^π₂[₀∫^−x+pi/2sin(x+y)dy]dx

Norbert: Nie ogarniam zapisu po znaku =

Mila: Bo tam ma być (+) przepraszam, to z powodu kopiowania. ₀∫^π₄ [₀∫^xsin(x+y)dy]dx+ _^π4∫^π₂ [₀∫^−x+pi/2sin(x+y)dy]dx

J: albo ... bez rozbijania na dwie całki ....zmieniasz kolejność całkowania:

	π
D: 0 ≤ y ≤
	4

	π
y ≤ x ≤ −x +
	2

= ∫₀^π/4[∫_y^−y+π/2(sin(x+y)dx]dy