Prosiłbym o jakieś wskazówki jak wykonać zadanie. Sev: W figurę ograniczoną parabolą o równaniu γ= −x²−6x+27 i osią odciętych wpisano prostokąt o najwiekszym polu.Oblicz to pole.

Janek191:

	6
p =		= − 3
	−2

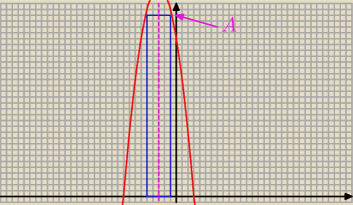
A = (x , − x² − 6 x + 27 ) P = 2*(x − p)*y = 2*( x + 3)*(− x² − 6 x +27) = −2 x³ − 12 x² + 54 x − 6 x² − 36 x +162 P( x) = − 2 x³ − 18 x² + 18 x + 162 więc P'(x) = − 6 x² − 36 x + 18 = − 6*( x² + 6 x − 3) = 0 ⇔ x² + 6 x − 3 = 0 Δ = 36 − 4*1*(−3) = 36 + 12 = 48 = 16*3 √Δ = 4√3

	− 6 + 4√3
x =		= − 3 + 2√3
	2

lub x = − 3 − 2√3 P''(x) = − 12 x − 36 więc P''( − 3 + 2√3) = 36 − 24 √3 − 36 < 0 więc funkcja P osiąga maksimum Wtedy pole prostokąta jest równe P = P( − 3 + 2√3 ) = ...

Sev: Dzięki za rozwiązanie zadania ale ja nie chciałem gotowca bo w ten sposób nie rozumie np. jak wyznaczyłeś sb to małe "p" skąd te liczby 6/−2 ? Jeszcze nwm skąd a raczej z jakiego wzoru jest to P=2*(x − p)*y samo liczenie jasne i łatwe... Jeszcze mam wątpliwość tak jak napisałeś P = P( − 3 + 2√3 ) = podstawiam pod P ( − 2 x³ − 18 x² + 18 x + 162 ) i zeby wyszło pole prostokąta trzeba to obliczyć lecz jak widze mój wynik to ani troche się nie powiela z wynikiem w książce mianowicie 96√3 W każdym razie dzięki za poświęcony czas.

Janek191:

	− b
p =
	2a

Janek191: 2*( x + 3) = 2*( − 3 + 2√3 + 3) = 4√3 y = − ( − 3 + 2√3)² − 6*( − 3 + 2√3) + 27 = = − ( 9 − 12 √3 + 12) + 18 − 12√3 + 27 = = − 21 + 12 √3 + 45 − 12√3 = 24 Pole P = 4√3*24 = 96√3 ==================

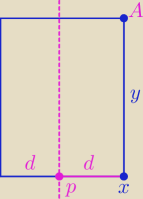
Janek191: p = − 3 A = ( x, y) = (x , − x² − 6 x + 27 ) Pole prostokąta obliczamy mnożąc jego szerokość przez długość Szerokość 2 d = 2 *( x − p) = 2*( x + 3) Długość ( wysokość ): y Zatem pole prostokąta P = 2*( x + 3)*y = 2*( x + 3)*( − x² − 6 x + 27 ) = ...

PW: Bardziej zrozumiałe rozważania o prostokącie oraz łatwiejsze rachunki będą, gdy zastosujemy przesunięcie wykresu. Funkcja f(x) = −x²−6x+27 = − (x+9)(x−3) ma wykres będący parabolą o miejscach zerowych −9 oraz 3. Po przesunięciu o wektor [3, 0] otrzymamy przystającą parabolę będącą wykresem funkcji h(x) = − (x+6)(x−6). Szukany prostokąt ma pole takie samo jak prostokąt o maksymalnym polu ograniczony wykresem h(x) i osią OX. Z uwagi na symetrię wykresu względem osi OY widać, że podstawą prostokąta musi być odcinek o podstawie [−x₀, x₀] na osi OX, mający długość 2x₀. Wysokość prostokąta jest równa h(x₀), zatem pole P opisuje funkcja P(x) = −2x·(x+6)(x−6) = − 2x³ − 72x, x∊(0, 6). Pochodna P'(x) jest określona wzorem P'(x) = − 6x² − 72, x∊(0, 6). Łatwo wyznaczamy punkt, w którym P'(x) zeruje się i wokół którego odpowiednio zmienia znak, a więc P(x) osiąga maksimum − jest to x₀ = √12 = 2√3. Wobec tego P_max = P(x₀) = P(2√3) = − 2·2√3((2√3)² − 36) = 4√3·24 = 96√3.

janek191: