Proszę o pomoc i wytłumaczenie. Jacek: Bardzo proszę o pomoc w tych zadaniach oraz wytłumaczenie. http://zapodaj.net/8867112bffc20.jpg.html −−−−> zadanie 6 http://zapodaj.net/eda2631d514f1.jpg.html

5-latek: jak przepiszsesz tutaj to pomoge

Jacek: Zadanie 6. Funkcja f określona jest wzorem f(x) = |x−1|−3, x należy do R. a) Oblicz miejsca zerowe funkcji f. b) Zapisz wzór funkcji f bez użycia znaku wartości bezwzględnej. c) Naszkicuj wykres funkcji f. d) Podaj zbiór wartości funkcji f. Zadanie 9. Na rysunku obok przedstawiony jest wykres funkcji f(x) = ax+5/x+1. Do wykresu funkcji f należy punkt A(−2,1) a) Odczytaj z wykresu dziedzinę i zbiór wartości funkcji f. b) Oblicz wartość a c) Dla wyznaczonej wartości a oblicz miejsce zerowe funkcji , a następnie odczytaj z wykresu , dla jakich argumentów funkcja f przyjmuje wartości nieujemne.

5-latek: Zadanie nr 9

	ax+5
mamy taki przepis na funkcje f(x)=y=
	x+1

Do jego wykresu należy punkt A(−2,1) czyli ten punkt spelnia równanie tej funkcji wiec podstawiamy do wzoru funkcji za x=−2 i y=1

	−2a+5
mamy 1=		to 1= −2a+5 wylicz z tego a
	−2+1

Jacek: a = −2 tak ?

5-latek: czy −2*(−2)+5=1?

Jacek: a = 2 ?

5-latek: Jacek nie zgaduj . Toz to podstawowka 1=−2a+5to 2a=5−1 to 2a=4 to a=2 OK czyli mamy taka funkcje jeśli wstawimy do jej wzoru za a= 2

	2x+5
y=
	x+1

Musimy teraz obliczyć jej miejsce zerowe wiec należy rozwiać równanie

2x+5
	=0
x+1

Odpowiedz mi na pytanie kiedy wyrażenie wymierne jest rowne 0 jeśli nie można dzielic przez 0 ?

Jacek: Aby wyznaczyć miejsce zerowe należy znać dziedzinę , więc x+1≠0 ⇔ R−{−1] 2x+5=0 ⇔2x=−5 x należy do R, bo nie istnieje liczba, która podniesiona do kwadratu daje −5. tak ?

5-latek: A czy tutaj w równaniu masz x² czy samo x ? wiec wylicz x i sprawdz z dziedzina

Jacek: Mój błąd. R−{−1} 2x+5=0⇔2x=−5 zatem x=−2,5

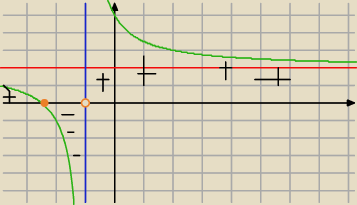
5-latek: teraz ma my odczytac z wykresu dla jakich argumentow funkcja f przyjmuje wartości nieujemne (czyli rowne o i >0 Musimy wiec narysować wykres tej funkcji a wiec należy ja przerksztalcic do postaci kanomicznej

	a
y=		+q
	x−p

mamy tak

2x+5		2(x+1)+3		3
	=		= 2+
x+1		x+1		x+1

Wiec nasza funkcja będzie miała taka postac kanoniczna

	3
y=		+2
	x+1

Widzimy z e asymtota pionowa ma równanie x=−1 a pozioma y=2 (z tego wzoru Widzisz ze wykres nigdy nie pokryje się a prosta x=−1 i y=2 Teraz patrz x=−2,5 to miejce zerowe wiec dla x∊(−2,5 1) funkcja ta osiąga wartości ujemne natomiast x∊(−∞,2,5> U(1,∞) wartości dodatnie

5-latek:

	2x+5
jeśli nie wiesz jak przeksztalcic		do postaci kanonicznej tak jak ja to zrobiłem to
	x+1

podziel sobie to pisemnie czyli 2x+5:x+1 i dostaniesz to samo

Jacek: Nie wiem co to jest asymtota. Realizuję program podstawowy i nie miałem tego. W zadaniu 9 , jest taki wykres : http://zapodaj.net/eda2631d514f1.jpg.html

5-latek: Jeśli masz funkcje wymierna to musisz wiedzieć co to jest asymptota jest to linia do której będzie się zblizal wykres funkcji po osi Ox i po osi OY ale się nidgy do nie zbliży Wiemy z edziedzine odczytujemy na osi OX Patrz teraz do jakiej linii zbliza się wykres po osi OX ? jakie ta linia ma równanie ? Wiec napisz jaka będzie dziedzina tej funkcji Najpierw to

Jacek: Spróbowałem sam to zrobić i Df−∞, −1,5) , a Zwf <−4,3>

5-latek: Może popatrz na ten przykład

5-latek: https://matematykaszkolna.pl/strona/167.html

Jacek: " Do wykresu funkcji f należy punkt A(−2,1), więc to jest ten wykres leżący w II i III ćwiartce. Tak mi się wydaje.

5-latek: Nie rozumiemy się . Z tegpo wykresu co masz w książce masz odczytac dziedzine i zbior wartości tej funkcji Wiec dziedzina to ? Odczytaj z osi OX TO samo zbior wartości to ? Odczytaj z osi OY

Jacek: Dobra, jestem kompletnym idiotą z matematyki. Jeśli możesz to rozwiąż mi po prostu te zadania, a ja je przepiszę. Nic do mnie nie trafia i ja się poddaje.

5-latek: Nie załamuj mnie Patrz na wykres z 11:30 Zobacz ze po osi OX wykres ten zbliza się to prostej x=−1 Wiec dziedzina tej funkcji będą wszystkie liczby rzeczywiste oprócz (−1) czyli D_f=R\{−1} Teraz zobacz ze po osi OY wykres ten zbliza się to prostej o równaniu y=2 Wiec zbior wartości tej funkcji to tez wszystkie liczby rzeczywiste oprócz 2 czyli Z_wf=R\{2} Popatrz na swój wykres z ksiaki i napisz jak będzie dziedzina i zbior wartości tej funkcji Popatrz tez na mój post z 12:01

5-latek: Narysuje CI na osobnym rysunku ten wykres z 11:30

Jacek: No ten wykres , do którego należy punkt A to jest funkcja f, a ten wykres y=f(x) to tez jest funkcja f ? Bo nie rozumiem. To dlaczego Zwf to R−{2]. Przez wartość 3, przechodzi linia.

5-latek: niebieska to x=−1 a zielona to y=2

Jacek: A u mnie na obrazku, ta zielona przechodzi przez 3.

5-latek: Realizujemy teraz podpunkt a) czyli masz odczytac dziedzine i zbior wartości z wykresu z książki

5-latek: No to jeśli przechodzi przez 3 to jaki będzie zbior wartości ?

Jacek: No tak. Ja rozumiem to tak : Jeżeli punkt A nalezy do wykresu funkcji f, to wykresem funkcji jest tylko i wyłącznie ten wykres po lewej stronie obrazka, a ten po prawej już się nie liczy bo to jest y.

Jacek: Df : R−[−1], a Zwf : R−{3} ?

5-latek: post 12:34 OK tylko popraw D_f=R−{−1} bo ten symbol [ ] oznacza czesc calkowita liczby Natomiast 12:33 to bzdury Nie można tak pisać

	a
Masz postac kanoniczna funkcji wymiernej taka y=		+q
	x−p

wiec asymtota pionowa ma równanie x= p (ale ze zmieniony znakiem Natomiast asymtota pozina ma równanie y=q Przykład

	2
y=		+3 to asymtota pionowa ma równanie x=5 a pozioma y=3
	x−5

	4
inny przykład		−7 to pionowa x=−8 poziona y=−7
	x+8

Jacek: A jak odczytać argumenty dla których wartości są nieujemne ?

5-latek: Nie skonczyles jeszcze jednego zadania a już się bierzesz za drugie

Jacek: Przecież napisałem dziedzinę i zbiór wartości , wartość a jest obliczona = 2 i teraz c) zostało.

5-latek: To przeczytaj sobie jeszcze raz dokładnie mój post 11:30 (ostatnie zdanie tylko zamiast dodatnie ma być oczywiście nieujemne . POza tym to zadanie masz już skończone bo te wartości nieujemne nie masz odcztyac z tego wykresu z książki tylko dla wyliczonej wartości a (i to już masz zrobione bo a=2

Jacek: No to (2,+∞) to będą nieujemne ?

Jacek: jeszcze miejsca zerowego nie mam

Jacek: Sorry, −2,5 to bylo Mzf

Jacek: W takim razie, wartości nieujemne to <−2,5,+∞) ?

5-latek: Patrzysz dla jakich argumentow (czyli x_ow wykres funkcji przecina os OX czyli wtedy wartośi funkcji sa rowne 0 i dla jakich x_ow wykres funkcji lezy nad osia OX bo wtedy wartości funkcji sa >0

Jacek: No to (−1,5, +∞) ?

5-latek: Patrz post 11:30 zobacz ze dla x∊(−2,5,1) wykres ten zielony lezy pod osia OX czyli wartości tej funkcji dla tych x_ow sa ujemne

Jacek: W takim razie (−1,+∞). Jeśli to jest źle to ja nie wiem, z ręką na sercu mówię że nie umiem...

5-latek: Jacek nie patrzysz na wykres z książki tylko na wykres z postu 11:30 (tego dotyczy podpunkt c) Z tego wykresu masz odczytac dla jakich x_ow wartości funkcji sa nieujemne .

Jacek: Nie wiem naprawdę.

5-latek: Patrz moje ostatnie zdanie post 11:30 (tylko teraz zauwazylem blad ma być oczywiście x∊(−∞,−2,5> U(1,∞) poprzednio napisałem 2,5 przepraszam .

Jacek: To teraz nic nie umiem, teraz wychodzi na to, że dziedziną jest (−∞,−2,5> U(1,∞) ?

5-latek: Teraz zobacz sobie na tym wykresie z 11:30 ze dla takich x_ow wartości funkcji sa nieujemne . Jeśli dalej nie będziesz rozumiał to pisz

Jacek: (−∞,−2,5> U(1,∞) są nieujemne bo leżą nad osią OX tak ?

5-latek: To może jeszcze inaczej . jak już tego nie zrozumiesz to nie wiem jak wytlumaczyc to Mamy wzor funkcji taki

	2x+5
f(x)=		wezmy np. x=−100
	x+1

	2*(−100)+5		−195
y=		=		to jest dodatnie >0 czyli wartość tej funkcji dla tego
	−100+1		−99

x>0 wezmy wezmy np. teraz x=−20

	2*(−20)+5		−35
y=		=		to >0 czyli y>0
	−20+1		−19

To teraz wezmy x=−2,5

2*(−2,5)+5		−5+5		0
	=		=		=0 czyli dla x=−2,5 wartość funkcji =0
−2,5+1		−1,5		−1,5

czyli wiodzisz ze jakakolwiek liczbe nie wizniesz z przedzialu x∊(−∞,2,5> to wartości tej funkcji będą dodatnie a dla x=−2,5 wartość funkcji =0 Wezmy teraz x∊(−2,5 −1 ) wezmy np. x=−2

	2*(−2)+5		1
y=		=		=−1 czyli wartość tej funkcji jest ujemna
	−2+1		−1

	−3+5
x=−1,5 to y=		<0 wartość funkcji ujemna
	−0,5

dla x=−1 wartość funkcji nie istnieje czyli dla x∊(−2,5 ,−1) watrtosci funkcji sa ujemne Teraz mamy przedzial od x∊(−1,∞) Sprawdz sobie ze jakakolwiek liczbe za x wstawisz z tego przedzialu do wzoru funkcji to y będzie >0 Ostateczna wersja dla x∊(−∞,−2,5>U(−1,∞) wartości tej funkcji sa nieujemne . To tylko było przez nieuwagę

5-latek: Tak wlasnie o to chodzi tylko popraw zamiast 1 to ma być (−1)

5-latek: Jeszcze jedno dla x=−1 wartość funkcji nie istniej bo dostaniemy dzielenie przez 0

5-latek: To sa takie chochliki

Jacek: Ok, a pomożesz mi z zdaniem 6 ?

5-latek: Tylko zjem obiad OK ?

Jacek: Wg mnie. a) miejscem zerowym jest 4 i −2

Jacek: Oki, oki smacznego

5-latek: Miejsca zerowe OK Zaloz nowy temat do tego zadania Pomin podpunkt a )bo jest OK