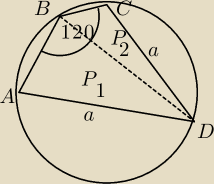
oblicz pole cxxx: Oblicz pole ABCD nie korzystając z tw sinusów lub cosinusów stosunek P₁ : P₂ =1:2

Kacper: Skorzystaj z tego, że |AC|=a

cxxx: zauwazyłem to mam policzone pole równobocznego ACD, ale potrzebuje pole ABC

cxxx: promien jest równy 6, zapomniałem dopisac

Mila: Sam narysowałeś i oznaczyłeś, czy przerysowałeś z książki? Na rysunku niezgodne wielkości trójkątów z proporcją. Może napisz dokładnie treść zadania.

Bogdan:

	1
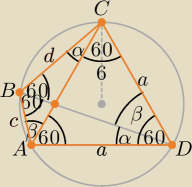
R = 6,		a√3 = 6 /*√3 ⇒ a = 6√3, β = 60o − α, |BD| = e
	3

	1		1
2*PABD = PBDC ⇒ 2*		*a*e*sinα =		*a*e*sinβ
	2		2

	√3		1
2sinα = sinβ ⇒ 2sinα = sin(60 − α) ⇒ 2sinα =		cosα −		sinα
	2		2

5		√3
	sinα =		cosα ⇒ 5sinα = √3cosα /2 ⇒ 25sin2α = 3cos2α
2		2

	3
25sin2α = 3(1 − sin2α) ⇒ sin2α =
	28

	√3
Pole trójkąta ABC: PABC = 2*62*sin120*sinα*sinβ = 72*		*sinα*2sinα =
	2

	3		54√3
= 72√3*sin2α = 72√3*		=
	28		7

Ponadto można w tym zadaniu wykazać, że d = 2c

cxxx: dziekuje odpowiedz jest prawidłowa. Z jakiego wzoru liczyles Pabc ?

Bogdan: Pole trójkąta przy danych miarach kątów wewnętrznych: α, β, γ oraz znanej długości promienia okręgu opisanego można obliczyć z zależności: P = 2R²*sinα*sinβ*sinγ

cxxx: a no tak czyli przy załozeniu ze d=2c mozna tez wyliczyc z c*2c*sin120 ?

Bogdan:

	1
Tak z małym zastrzeżeniem, P =		c*2c*sin120o, tu trzeba jeszcze wyznaczyć
	2

długość c