Oblicz angelika: 1. Dwa boki trójkąta mają długości 2 i 3, a odcinek dwusiecznej kąta między nimi zawarty w tym trójkącie ma długość 2. Oblicz pole trojkąta. 2. Oblicz pole trójkąta, którego dwa boki mają długości 6 i 4, a długość środkowej opuszczonej na trzeci bok jest równa 3. Dziękuję

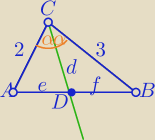
Mila: |CD|=d=2

1		1		1
	*2*2sinα+		*2*3*sinα=		*2*3*sin(2α)⇔
2		2		2

2sinα+3sinα=3sin(2α)⇔ 5sinα=6*sinα*cosα

	5
cosα=
	6

	25
sin2α=1−
	36

	11
sin2α=
	36

	√11
sinα=
	6

	5		√11
2*sinα*cosα=2*		*		⇔
	6		6

	5√11
sin(2α)=
	18

	1		5√11
PΔABC=		*2*3*sin(2α)=3*
	2		18

	15√11
PΔABC=
	18

=================

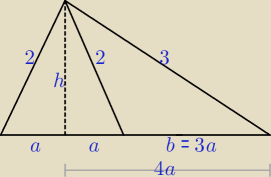Bogdan: Moja propozycja rozwiązania (bez trygonometrii, tylko Pitagoras):

2		3
	=		⇒ b = 3a
2a		b

16a² + h² = 9 a² + h² = 4

	1		1		11
15a2 = 5 ⇒ a2 =		i h2 = 4 −		=
	3		3		3

	1		25		25		1		11
Pole trójkąta P: P2 = (		*5a*h)2 =		a2h2 =		*		*
	2		4		4		3		3

	5√11
P =
	2*3

Mila: A ja nie uprościłam na końcu. Ładne rozwiązanie Bogdanie.

Bogdan:

Eta:

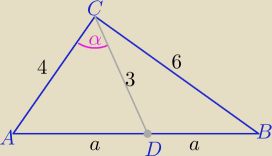Eta: Środkowa dzieli trójkąt na dwa trójkąty o równych polach to P(ABC)= 2P(ADC) 4|CD|²= 2*4²+2*6²−4a² ⇒ 9=8+18−a²⇒ a²=17

	16+9−17		1		1		2√2
cosα=		=		to sinα=√1−		=
	2*4*3		3		9		3

P(ABC)= 4*3*sinα= 8√2

Bogdan: też ładnie

Eta:

Kacper:

Ajtek: Ale się popisują

Eta: