Funkcja homograficzna Monika: Funkcja F(x) = (ax+b)/(x+c , gdzie ac – b ≠0 i x ≠ –c, jest monotoniczna w przedziałach (−∞,3), (3, +∞), zbiorem wartości funkcji jest zbiór R – {2}, zaś jej miejscem zerowym jest liczba –2,5. Wyznacz wartości współczynników a, b, c. Następnie: a) podaj zbiór tych argumentów, dla których funkcja przyjmuje wartości nieujemne; b) naszkicuj wykres funkcji G(x) = F(|x|) i na jego podstawie zbadaj liczbę rozwiązań równania G(x) = m, gdzie m ∊R. Z monotoniczności wywnioskowałam, że dziedziną są rzeczywiste liczby oprócz liczby 3. Skoro zbiót wartości to rzeczywiste bez liczby 2, to wektor przesunięcia wynosi [3,2]. Czyli p=3, a q=2. Podstawiłam sobie miejsce zerowe i wyszło mi 0=(−2,5a+b)/(−2,5+c) I kompletnie nie wiem, co dalej z tym zrobić. Proszę o pomoc.

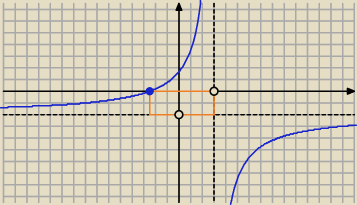
asior: Pole wyróżnionego prostokąta P = 11

	11		−2x − 5
Funkcja homograficzna f(x) =		− 2 =
	x − 3		x − 3

Monika: A jak wyznaczyć a, b, c?