potrzebuje pomocy z tym zadaniem
olka: Przekątne trapezu równoramiennego przecinają się pod katem prostym.
Oblicz odległości punktu przecięcia przekątnych od ramion tego trapezu,
jeśli jego podstawy maja długości 4 cm i 12 cm.
29 maj 19:26
Tadeusz:
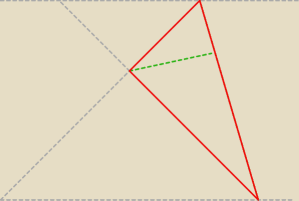
− policz jak dzielą się przekątne
− policz długość boku trapezu
− policz pole trójkąta z odcinków przekątnej a potem z boku i szukanej odległości
29 maj 19:41
prosta:
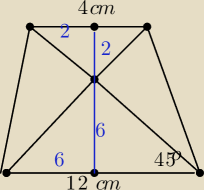
29 maj 19:42
Marek216:
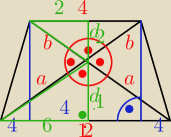
a=
√6 i b =
√2
Dł. przekątnej
√6 +
√2
Poradzisz sobie dalej ?
29 maj 19:43
Marek216: a i b źle Ci napisałem a to 6√2 a b to 2√2 sry z pośpiechu.
29 maj 19:45
prosta:
długość przekątnej: 8√2
29 maj 19:46
Tadeusz:
... oj Ludziska ... odległości punktu przecięcia się przekątnych od
ramion trapezu −

29 maj 19:47
Marek216: Dlatego napisałem czy poradzi sobie dalej

29 maj 19:48
Marek216: prosta wiem poprawiłem się.
29 maj 19:48
prosta:
długość ramienia: 4√5
d− szukana odległość
4√5d=(2√2)(6√2)
d=1,2√2
29 maj 19:50
Marek216: Można narysować w układzie współrzędnych i ustalić punkt przecięcia i końce ramion i wyznaczyć
odległość punktu od prostej bez kombinowania.
29 maj 19:50
prosta:
d= .... moje obliczenie do poprawki
29 maj 19:52
Marek216: Podam sposób dla mojego rysunku P − punkt przecięcia przekątnych , A,B końce odcinka tworzącego
ramię (prawe), początek układu wsp. to lewy dolny róg trapezu.
P=(6,d1) A = (8,d1+d2) B = (12,0)> Wyznaczasz równanie prostej AB i liczysz odleglość prostej
zawierającej AB od punktu P
29 maj 19:55
olka: A mógłbyś jednak mi to w całości obliczyć, bo serio jestem kiepska z matmy

byłabym ogromnie
wdzięczna
29 maj 20:11
Marek216: Do godziny postaram się zrobić, zrobię na 2 sposoby napisze ci ten krótszy.
29 maj 20:14
Marek216: Muszę wyjść na chwilę z domu.
29 maj 20:15
olka: Jasne, dzięki, będę ogromnie wdzięczna bo z tego mam sprawdzian

a mogę dodać, że odpowiedzi do 6
√5/5 cm i 6
√5/5 cm
29 maj 20:20
Eta:
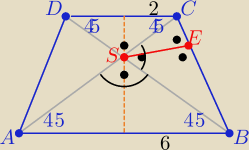
|SB|=6
√2, |SC|=2
√2 |CB|=
√(2√2)2+(6√2)2=
√80=4
√5
| | |SC|*|SB| | | 2√2*6√2 | | 6 | | 6√5 | |
SF=|SE= |
| = |
| = |
| = |
| |
| | |CB| | | 4√5 | | √5 | | 5 | |
29 maj 20:49
olek:
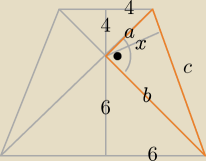
| | ab | | 4√2 * 6√2 | | 24 | |
x = |
| = |
| = |
| |
| | c | | √32 + 72 | | √26 | |
29 maj 20:57
Eta:
Olek

a=
2√2
29 maj 21:02
Marek216: O widzę, że Eta już rozwiązała

, Olka jeżeli nie rozumiesz ostatniej linijki (Ety) to
wynika ona z wzorów na pole trójkąta BCS (oznaczenia Ety).
29 maj 21:07
olek:
| | 2√2 * 6√2 | | 6 | |
Jeśli zamiast 4 weźmiemy 2, to x = |
| = |
| |
| | √8 + 72 | | √5 | |
29 maj 21:24
Eta: I o to chodzi

29 maj 21:28
 − policz jak dzielą się przekątne
− policz długość boku trapezu
− policz pole trójkąta z odcinków przekątnej a potem z boku i szukanej odległości
− policz jak dzielą się przekątne
− policz długość boku trapezu
− policz pole trójkąta z odcinków przekątnej a potem z boku i szukanej odległości

 a=√6 i b = √2
Dł. przekątnej √6 + √2
Poradzisz sobie dalej ?
a=√6 i b = √2
Dł. przekątnej √6 + √2
Poradzisz sobie dalej ?


 byłabym ogromnie
wdzięczna
byłabym ogromnie
wdzięczna
 a mogę dodać, że odpowiedzi do 6√5/5 cm i 6√5/5 cm
a mogę dodać, że odpowiedzi do 6√5/5 cm i 6√5/5 cm
 |SB|=6√2, |SC|=2√2 |CB|=√(2√2)2+(6√2)2= √80=4√5
|SB|=6√2, |SC|=2√2 |CB|=√(2√2)2+(6√2)2= √80=4√5

 a= 2√2
a= 2√2
 , Olka jeżeli nie rozumiesz ostatniej linijki (Ety) to
wynika ona z wzorów na pole trójkąta BCS (oznaczenia Ety).
, Olka jeżeli nie rozumiesz ostatniej linijki (Ety) to
wynika ona z wzorów na pole trójkąta BCS (oznaczenia Ety).
