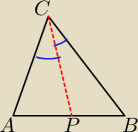
 Niech [X] oznacza pole figury X
Oznaczmy <ACP=α wtedy <BCP=α
[APC]=1/2 AC*CP*sinα
[BPC]=1/2 BC*CP*sinα
Niech [X] oznacza pole figury X
Oznaczmy <ACP=α wtedy <BCP=α
[APC]=1/2 AC*CP*sinα
[BPC]=1/2 BC*CP*sinα
| [APC] | AC | ||
= | |||
| [BPC] | BC |
| [APC] | AP | |||
Z drugiej strony | = | , bo trójkąty APC i BPC mają wspólną wysokość | ||
| [BPC] | PB |
| AC | AP | |||
Stąd dostajemy | = | , a to jest równoważne tezie. | ||
| BC | PB |