help
Yazz:
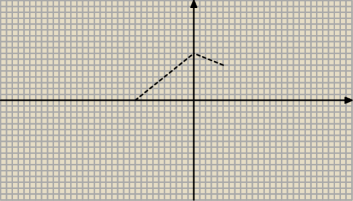
Co zrobić jeśli narysowany wykres, to funkcja f(x) a musze przeksztalcic go na g(x)=f(1−|x|)
Opiszcie krok po kroku, jestem "kumaty".
29 maj 18:16
Kacper:
Jak jesteś "kumaty", to dlaczego nie umiesz?

29 maj 18:17
Janek191:
Oblicz

g( −10) , g(0) i g( 5)
29 maj 18:19
Yazz: g(−10)=f(1−|x|)
w tym momencie sie zatrzymuje xd
nie prawcie mi jakichs kazan, tylko wytlumaczcie, prosze

29 maj 20:53
Marek216:
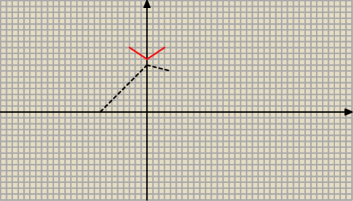
Na moje oko takie coś wyjdzie, czerwony wykres (symetria OY)
29 maj 21:23
Marek216:
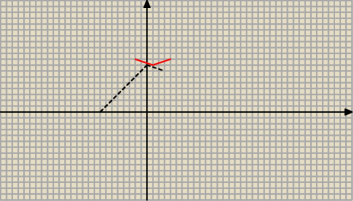
Sry, przesunięcie poziome a nie pionowe *
29 maj 21:24
Marek216: Kuźwa coś nie tak

, porypałem.
29 maj 21:26
Yazz: Ktoś będzie tak miły i pomoże?
30 maj 09:19
Yazz: Ktokolwiek?

30 maj 23:23
Viper: Najpierw zajmij się wart. bezwzględną, czyli to co masz na lewo od osi OY "znika", a to co jest
po prawej zostaje i odbija się na lewo (wychodzi taki daszek). Później przesuwasz o 1 w prawo
i gotowe.
Ale nie jestem pewien

31 maj 18:09
Yazz: No właśnie nie

Zna się ktoś na tym? Jest to aż tak trudne?

31 maj 19:12
Mila:
f(1−|x|)=f(−|x|+1))
1) f(x) − już masz wykres
→SOY⇒f(−x)→
→T[1,0] ⇒f(−x+1)→SOY wykresu z prawej strony, o lewej zapominasz⇒f(−|x|+1)
31 maj 20:19
Viper: Skoro jest f(−x+1) to nie powinno być przesunięcie o wektor [−1,0]?
A tak btw. to jak się wyznacza kolejność tych przekształceń? Bo nie wiem czy wart. bezwzględną
x zawsze na końcu, czy w zależności od sytuacji?
31 maj 20:46
Mila:
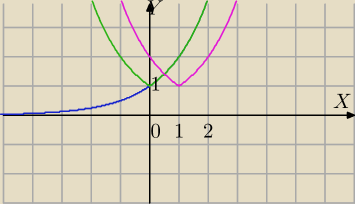
Jeśli masz wykres f(−x) to po translacji o wektor [1,0] otrzymujesz wykres funkcji o wzorze:
f(−(x−1))=f(−x+1) czyli to co chcemy otrzymać.
Kolejność przekształceń w zależności od sytuacji.
Przykład I
f(x)=2
|x−1|
kolejność
y=2x}}→S
OY tego co z prawej⇒
y=2|x|→T{[1,0]}⇔
y=2|x−1|
W następnym wpisie będzie:
f(x)=2
|x|−1
31 maj 20:59
Mila:
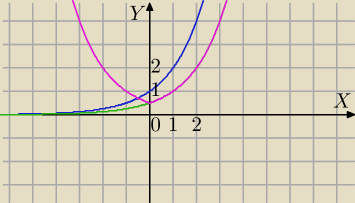
f(x)=2
|x|−1
1) y=2
x→T
1,0]⇒
g(x)=2x−1→S
OY tego co z prawej⇒
f(x)=2|x|−1
31 maj 21:07
Viper: Dzięki wielkie Mila za wyjaśnienia i dobre przykłady (jutro spr. z funkcji wykładniczej

).
Ogólnie to nie jest takie złe, ale ani w szkole, ani w książce od matmy nie było nic o
kolejności.
Teraz już czaję kiedy, które najpierw, thx

31 maj 21:34
Mila:
Tak, to nie jest wyjaśnione w podręcznikach, a nauczyciele lubią dawać takie zadania na
sprawdzianie .
Z tym, że z tymi przesunięciami w funkcjach trygonometrycznych to jeszcze inny problem
występuje.
( chodzi o powinowactwo).
31 maj 21:53
Yazz: kiedy to co zrobiłeś, jest prawdopodobnie złe − odpowiedzi w książce się nie zgadzają

dodatkowo Pan Profesor na lekcji tłumaczył, że trzeba to rozpisać:
−x+1 dla x <0
x+1 dla x≥0
1 cze 02:29
Mila:
Co jest źle?
O którym rozwiązaniu mówisz? I Jakie masz odpowiedzi w książce?
1 cze 16:55
1 cze 18:22
Mila:
Nie mogę odczytać jakie jest polecenie.
Na rysunku jest wykres f(x) tak?
Należy otrzymać wykres g(x)=f(2−|x|) tak?
1 cze 18:52
Yazz: tak.
1 cze 18:58
Mila:
No to zrób tak, jak napisałam o 20:19. wyjdzie dobrze.
Poza tym, to podałeś: g(x)=(1−|x|) i tak próbował Marek. Nie sprawdzałam jego rozwiązania,
podałam sposób ogólny.
Jeśli Ci nie wyjdzie, to narysuję. Napisz.
1 cze 19:04
prosta:
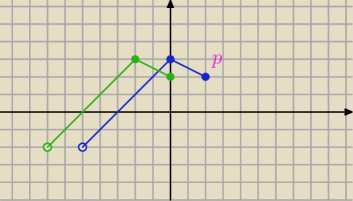
1. f(x) −−−−−−−>f(2+x) przesunięcie dwiuie jednostki w lewo
1 cze 19:56
prosta:
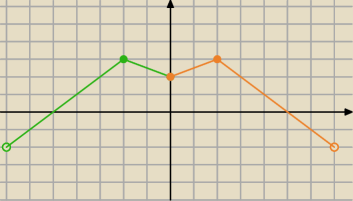
2. f(x+2) −−−−> f(−x+2) odbicie symetryczne względem osi Oy
1 cze 19:59
prosta:
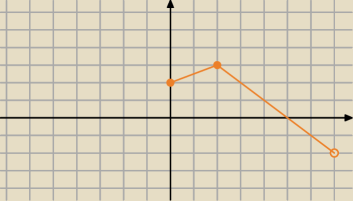
3. f(−x+2) −−−−−−> f(−|x|+2)
1 cze 20:01
prosta:
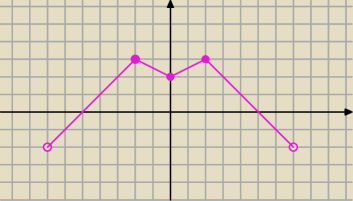
1 cze 20:02
Yazz: To ja juz sam nie wiem co mial na mysli Pan Profesor..
Moze chodzilo o f(|1−|x||) ? Czy wtedy nalezaloby rozpisac dla x<0 i x≥0?
1 cze 20:13
prosta:
można rozpisywać...ale tutaj nie ma wzoru...więc bardzo ogólnie to wyjdzie
1 cze 20:15
Mila:
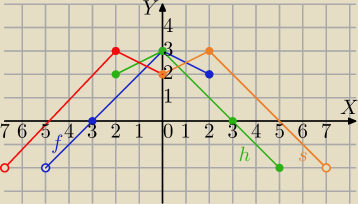
Najpierw symetria.
1) f(x)→S
OY⇒otrzymujesz wykres h(x)=f(−x)
2)h(x)=f(−x)→T
[2,0]⇒otrzymujesz wykres s(x)=f(−x+2)
3)S
OY pomarańczowego wykresu⇒otrzymujesz wykres g(x)=f(−|x|+2)=f(2−|x|)
Ten wykres składa się z dwóch gałązek − pomarańczowej i czerwonej.
Dziedzina: (−7,7)
zbiór wartości (−2,3>
1 cze 20:16
Yazz: Mila, tylko, że przesuwanie o wektor [2,0] daje przesunięcie o dwa w lewo, ponieważ:
f(x−q)+p to przesunięcie f(x) o wektor [q,p]
1 cze 20:28
Mila:
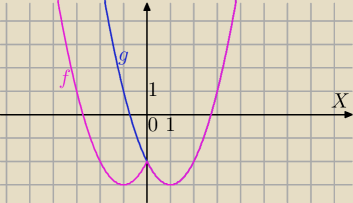 Yazz
Yazz masz dwa przykłady przekształcenia wykresu funkcji wykładniczej.
Możesz to zrobić rozpisując, jak Profesor tłumaczył, albo tak jak podałam. Wyjdzie to samo
Patrz przykłady 20:59 i 21:07
drugi sposób jest w wielu przypadkach bardzo użyteczny.
np.
Wykres funkcji:
f(x)=x
2−2|x|−2
1) rysujesz wykres g(x)=x
2−2x−2
2) Symetria S
OY tej części wykresu , która odpowiada x≥0,
otrzymujesz wykres f(x)=X
2−2|x|−2
1 cze 20:28
Mila:
Przesuwasz wykres f(−x) o wektor [2,0] to otrzymasz wykres funkcji:
f(−(x−2))+0=f(−x+2) czyli to, co chcemy.
1 cze 20:31
Yazz: A co gdy funkcja f bedzie np:
3 dla x<1
2x+3 dla x <1,2)
3x−2 dla x≥2
?
Czuje sie jak debil xd przede mna kartkowka i sprawdzian, ktorych nie pisalem, a ten przyklad
jest tym, ktory zabiera mi szanse na 5 na koniec.
1 cze 21:22
Mila:
Jakie polecenie do zadania?
1 cze 21:24
Yazz: Dajmy takie samo g(x)=f(1−|x|)
1 cze 21:26
Mila:
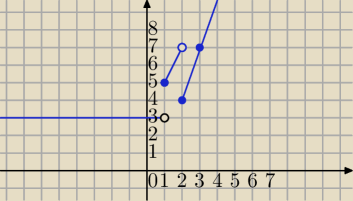
1) rysujesz wykres f(x)
2) Symetria względem OY otrzymasz f(−x)
3) Translacja o wektor [1,0] otrzymasz f(−x+1)
4) S
OY wykresu odpowiadającego x≥0⇒g(x)=f(−|x|+1)
W której klasie jesteś i jaki podręcznik Cię obowiązuje?
1 cze 21:44
Mila:
Jeśli wiesz , czego nie wiesz, to już jest dużo warte.
1 cze 21:45
Mila:
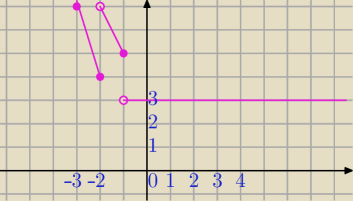
f(−x)
1 cze 21:56
Yazz: Wlasnie jak czegos nie wiem, to sie chce dowiedziec, szczegolnie jesli chodzi o matematyke.
Podrecznik MATeMAtyka wojciech babinski, lech chanko, dorota ponczek klasa 1.
A co z badaniem roznowartosciowosci funkcji? Sa jakies zaleznosci miedzy roznowartosciowoscis a
parzystoscia? Oprocz tej ze funkcja parzysta jest nieroznowartosciowa
1 cze 21:58
Mila:
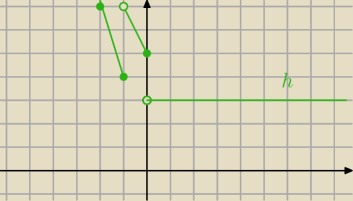
Translacja wykresu f(−x) o wektor [1,0] otrzymasz h(x)= f(−x+1)
1 cze 22:00
Mila:
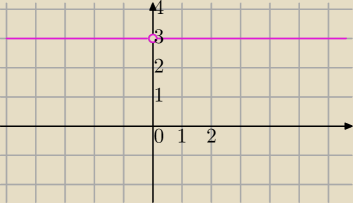
f(1−|x|)
1 cze 22:01
Mila:
Musisz napisać konkretne zadanie, najlepiej z podręcznika , bez własnych interpretacji.
1 cze 22:03
Yazz: Rysunek ten co u gory.
dziedzina funkcji f jest przedzial (−5;2> podaj dziedzine i naszkicuj g(x)=f(|x|−3)
1 cze 22:06
Yazz: Chodzi o to, ze przykladow z (|x|−jakasliczba) lub odwrotnie, jest malo, a mianowicie 3, z
czego do zadnego z nich nie ma narysowanego wykresu w odpowiedziach (gdyby byl, to bym ogarnal
to sam)
1 cze 22:08
Mila:
Z której godziny rysunek?
Ten z linka?
1 cze 22:09
Yazz: Tak
1 cze 22:10
Mila:
Postępuj tak jak w przepisie z 21:07, tylko translacja o wektor [3,0].
Zrób samodzielnie, potem sprawdzę.
1 cze 22:12
Yazz: Jestem na komie wiec raczej slabo XD
napisze w punktach:
1.przesuniecie O wektor [3,0]
2. Odbicie x≥0 przez OY
1 cze 22:16
Mila:
1) po translacji otrzymasz f(x−3)
2) po symetrii otrzymasz wykres : f(|x|−3)
i jaka dziedzina?
Mam narysować?
1 cze 22:19
Yazz: Dziedzina od −5 do 5 zamkniete. Bedzie takie jakby M
mozesz narysowac
1 cze 22:23
Mila:
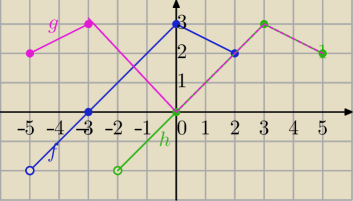
1) f(x)
2) h(x)=f(x−3)
3)g(x)=f(|x|−3)
D=<−5,5>
Zw
f=<0,3>
Funkcja nie jest różnowartościowa
g(x)− funkcja parzysta (Oś OY jest osią symetrii wykresu>
1 cze 22:44
Mila:
Zwg=<0,3>
1 cze 22:54
Mila:
I na koniec pisze się " dziękuję".
1 cze 23:28
Yazz: Okej dziekuje, ale poki co wciaz nie jestem pewny czy mi sie powiedzie

2 cze 15:44
Mila:
Rozwiązuj zadania , masz być przekonany o prawidłowości rozwiązania.
2 cze 16:54
 Co zrobić jeśli narysowany wykres, to funkcja f(x) a musze przeksztalcic go na g(x)=f(1−|x|)
Opiszcie krok po kroku, jestem "kumaty".
Co zrobić jeśli narysowany wykres, to funkcja f(x) a musze przeksztalcic go na g(x)=f(1−|x|)
Opiszcie krok po kroku, jestem "kumaty".

 g( −10) , g(0) i g( 5)
g( −10) , g(0) i g( 5)

 Na moje oko takie coś wyjdzie, czerwony wykres (symetria OY)
Na moje oko takie coś wyjdzie, czerwony wykres (symetria OY)
 Sry, przesunięcie poziome a nie pionowe *
Sry, przesunięcie poziome a nie pionowe *
 , porypałem.
, porypałem.


 Zna się ktoś na tym? Jest to aż tak trudne?
Zna się ktoś na tym? Jest to aż tak trudne? 
 Jeśli masz wykres f(−x) to po translacji o wektor [1,0] otrzymujesz wykres funkcji o wzorze:
f(−(x−1))=f(−x+1) czyli to co chcemy otrzymać.
Kolejność przekształceń w zależności od sytuacji.
Przykład I
f(x)=2|x−1|
kolejność
y=2x}}→SOY tego co z prawej⇒y=2|x|→T{[1,0]}⇔y=2|x−1|
W następnym wpisie będzie:
f(x)=2|x|−1
Jeśli masz wykres f(−x) to po translacji o wektor [1,0] otrzymujesz wykres funkcji o wzorze:
f(−(x−1))=f(−x+1) czyli to co chcemy otrzymać.
Kolejność przekształceń w zależności od sytuacji.
Przykład I
f(x)=2|x−1|
kolejność
y=2x}}→SOY tego co z prawej⇒y=2|x|→T{[1,0]}⇔y=2|x−1|
W następnym wpisie będzie:
f(x)=2|x|−1
 f(x)=2|x|−1
1) y=2x→T1,0]⇒g(x)=2x−1→SOY tego co z prawej⇒f(x)=2|x|−1
f(x)=2|x|−1
1) y=2x→T1,0]⇒g(x)=2x−1→SOY tego co z prawej⇒f(x)=2|x|−1
 ).
Ogólnie to nie jest takie złe, ale ani w szkole, ani w książce od matmy nie było nic o
kolejności.
Teraz już czaję kiedy, które najpierw, thx
).
Ogólnie to nie jest takie złe, ale ani w szkole, ani w książce od matmy nie było nic o
kolejności.
Teraz już czaję kiedy, które najpierw, thx 
 dodatkowo Pan Profesor na lekcji tłumaczył, że trzeba to rozpisać:
−x+1 dla x <0
x+1 dla x≥0
dodatkowo Pan Profesor na lekcji tłumaczył, że trzeba to rozpisać:
−x+1 dla x <0
x+1 dla x≥0
 1. f(x) −−−−−−−>f(2+x) przesunięcie dwiuie jednostki w lewo
1. f(x) −−−−−−−>f(2+x) przesunięcie dwiuie jednostki w lewo
 2. f(x+2) −−−−> f(−x+2) odbicie symetryczne względem osi Oy
2. f(x+2) −−−−> f(−x+2) odbicie symetryczne względem osi Oy
 3. f(−x+2) −−−−−−> f(−|x|+2)
3. f(−x+2) −−−−−−> f(−|x|+2)

 Najpierw symetria.
1) f(x)→SOY⇒otrzymujesz wykres h(x)=f(−x)
2)h(x)=f(−x)→T[2,0]⇒otrzymujesz wykres s(x)=f(−x+2)
3)SOY pomarańczowego wykresu⇒otrzymujesz wykres g(x)=f(−|x|+2)=f(2−|x|)
Ten wykres składa się z dwóch gałązek − pomarańczowej i czerwonej.
Dziedzina: (−7,7)
zbiór wartości (−2,3>
Najpierw symetria.
1) f(x)→SOY⇒otrzymujesz wykres h(x)=f(−x)
2)h(x)=f(−x)→T[2,0]⇒otrzymujesz wykres s(x)=f(−x+2)
3)SOY pomarańczowego wykresu⇒otrzymujesz wykres g(x)=f(−|x|+2)=f(2−|x|)
Ten wykres składa się z dwóch gałązek − pomarańczowej i czerwonej.
Dziedzina: (−7,7)
zbiór wartości (−2,3>
 Yazz masz dwa przykłady przekształcenia wykresu funkcji wykładniczej.
Możesz to zrobić rozpisując, jak Profesor tłumaczył, albo tak jak podałam. Wyjdzie to samo
Patrz przykłady 20:59 i 21:07
drugi sposób jest w wielu przypadkach bardzo użyteczny.
np.
Wykres funkcji:
f(x)=x2−2|x|−2
1) rysujesz wykres g(x)=x2−2x−2
2) Symetria SOY tej części wykresu , która odpowiada x≥0,
otrzymujesz wykres f(x)=X2−2|x|−2
Yazz masz dwa przykłady przekształcenia wykresu funkcji wykładniczej.
Możesz to zrobić rozpisując, jak Profesor tłumaczył, albo tak jak podałam. Wyjdzie to samo
Patrz przykłady 20:59 i 21:07
drugi sposób jest w wielu przypadkach bardzo użyteczny.
np.
Wykres funkcji:
f(x)=x2−2|x|−2
1) rysujesz wykres g(x)=x2−2x−2
2) Symetria SOY tej części wykresu , która odpowiada x≥0,
otrzymujesz wykres f(x)=X2−2|x|−2
 1) rysujesz wykres f(x)
2) Symetria względem OY otrzymasz f(−x)
3) Translacja o wektor [1,0] otrzymasz f(−x+1)
4) SOY wykresu odpowiadającego x≥0⇒g(x)=f(−|x|+1)
W której klasie jesteś i jaki podręcznik Cię obowiązuje?
1) rysujesz wykres f(x)
2) Symetria względem OY otrzymasz f(−x)
3) Translacja o wektor [1,0] otrzymasz f(−x+1)
4) SOY wykresu odpowiadającego x≥0⇒g(x)=f(−|x|+1)
W której klasie jesteś i jaki podręcznik Cię obowiązuje?
 f(−x)
f(−x)
 Translacja wykresu f(−x) o wektor [1,0] otrzymasz h(x)= f(−x+1)
Translacja wykresu f(−x) o wektor [1,0] otrzymasz h(x)= f(−x+1)
 f(1−|x|)
f(1−|x|)
 1) f(x)
2) h(x)=f(x−3)
3)g(x)=f(|x|−3)
D=<−5,5>
Zwf=<0,3>
Funkcja nie jest różnowartościowa
g(x)− funkcja parzysta (Oś OY jest osią symetrii wykresu>
1) f(x)
2) h(x)=f(x−3)
3)g(x)=f(|x|−3)
D=<−5,5>
Zwf=<0,3>
Funkcja nie jest różnowartościowa
g(x)− funkcja parzysta (Oś OY jest osią symetrii wykresu>
