planimetria Emshya: Dany jest trapez prostokątny ABCD o kątach prostych przy wierzchołkach A i D opisany na okręgu. Oblicz pole trapezu jeśli wiadomo że SB=8 i SC=6 gdzie S jest środkiem okręgu. Od czego zacząć bo jakoś nie mam pomysłu?

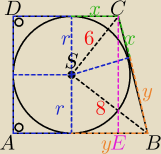
vaultboy: Polecam zacząć od zrobienia rysunku. Jeśli oznaczymy przez r promień naszego okręgu to dostaniemy, że: r²+x²=6² (Pitagoras) r²+y²=8² (j.w.) Zrzutujmy C na AB i oznaczmy ten rzut przez E. Wtedy CE=AD=2r oraz CE²+EB²=CB² czyli (2r)²+(y−x)²=(x+y)² Masz układ 3 równań z 3 niewiadomymi. Dalej chyba sam(a) dasz radę.

pigor: ..., ΔBSC − prostokątny (... łatwo wykazać), więc z warunków zadania |BC|= 10 i r *10= 6 *8 ⇒ r= 4,8 i x²= 6²−r² ⇒ x²= 1,2*10,8 ⇒ ⇒ x= 3,6, zatem P_ABCD= ¹₂(r+x)*2r= ¹₂*8,4*2*4,8= 40,32 . ...

Mila: ΔCSB− Δprostokątny (łatwo możesz wykazać) |CB|²=6²+8² |CB|=10

	1		1
PΔCSB=		*6*8=		*r*10
	2		2

6*8=10r r=4,8 h=|AD|=2r=9,6 Sumy długości boków przeciwległych są równe. |AB|+|DC|=|BC|+|AD| |BC|+|AD|=10+9,6

	19,6
PABCD=		*9,6
	2

Emshya: ok dziękii

pigor: ..., a ja... zapomniałem we wzorze na pole o dolnej podstawie trapezu..

masakra: "Masz układ 3 równań z 3 niewiadomym" wg niejakiego vaultboy − do dupy z taką poradą.

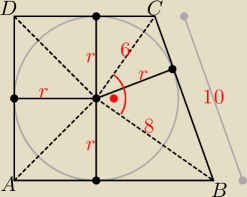
Bogdan: Szkic.

	6*8
|BC| = √62 + 82 = 10 i r =		= 4,8, pole trapezu P = 6*8 + 2*4,82 = 94,8
	10

vaultboy: masakra: "Masz układ 3 równań z 3 niewiadomym" wg niejakiego vaultboy − do dupy z taką poradą. Dziękuje za krytykę. Rozwiązanie: r²+x²=6² r²+y²=8² r²=xy Dostajemy xy+x²=6² (1) xy+y²=8² (2) sumując otrzymuję x²+2xy+y²=100 czyli (x+y)²=100 ⇒ x+y=10 odejmując (1) i (2) otrzymuję (y−x)(x+y)=64−36=28 czyli y−x=2,8 Stąd można wyliczyć x i y oraz po wyliczeniu x,y dostajemy r