Matematyka dyskretna. Oblicz ilu uczniów liczy klasa
Lukas: Witam prosiłbym o wskazówkę jak rozwiązywać tego typu zadania:
W pewnej klasie uczniowie zdają egzamin z matematyki, angielski lub polski. 20 uczniów zdaje
egzamin z matematyki, 16 z polskiego 14 z angielskiego. Ilu uczniów jest w tej klasie, jeżeli
nikt
nie zdaje egzaminu ze wszystkich trzech przedmiotów, 10 uczniów zdaje matematykę i angielski, 6
matematykę i polski, a 4 angielski i polski?
Pozdrawiam,
28 maj 21:44
Janek191:
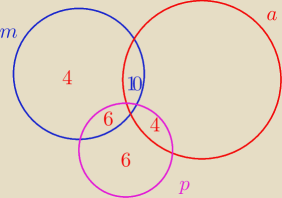
28 maj 21:51
Lukas: Rozumiem, że odpowiedzią jest wartość 10? Skąd ona się tam wzięła? wg. jakiej zasady?
28 maj 21:53
Janek191:
Dodaj te wszystkie liczby

28 maj 21:54
Bogdan:
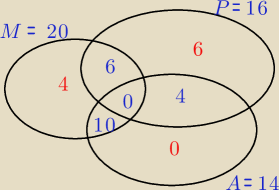
28 maj 21:55
Bogdan:

28 maj 21:56
Lukas: 30 ? Jeżeli wynikiem jest 30 to otrzymałem już taką wartość jednak nie wiem czy moje
rozwiązanie jest poprawne. Dodałem wszystkich piszących 20+14+16 i odjąłem od nich wartość
10+6+4 wtedy również otrzymamy 30.
28 maj 21:57
Janek191:
Ok

28 maj 22:00
PW: Argumentacja do niczego.
20+16+14 = 50
to liczba przeprowadzonych egzaminów, a nie "piszących".
2·(10+6+4) = 40
to liczba egzaminów odbytych przez uczniów zdających dwa przedmioty.
(1) 50 − 40 = 10
to liczba uczniów zdających tylko jeden egzamin.
Zdający tylko jeden egzamin plus zdający dwa egzaminy
10+(10+6+4) = 30
to liczba wszystkich uczniów.
Obawiam się, że to gimnazjum, a nie "matematyka dyskretna".
28 maj 22:19




