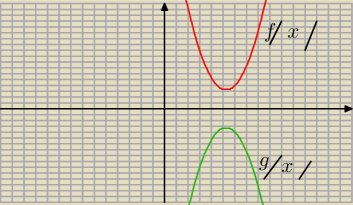
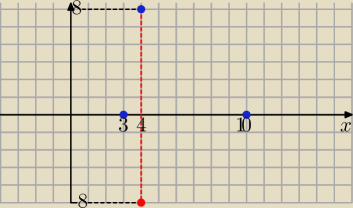
Symetria osiowa względem osi OX Mia: Funkcja f ma dwa miejsca zerowe 3 oraz 10, dla argumentu 4 przyjmuje wartość (−8). Wykres funkcji g otrzymaliśmy po przekształceniu wykresu funkcji f przez symetrię osiową względem osi OX. Podaj wartość: g(3), g(10), g(4). Proszę pomóżcie

Janek191: Pytanie − jaką funkcją jest f ? Kwadratową ?

Martiminiano: Oto samo właśnie pytałem.

Madzia: Wiemy, że f(3)=0 f(10)=0 f(4)=−8 Gdy przekształcamy wykres przez symetrię OX, wartości funkcji zmieniają się na przeciwne, więc logicznie można wydedukować ,że g(3)=0 g(10)=0 g(4)=8

Mia: Nie wiem, kwadratowej jeszcze nie miałam.. zaczęłam to robić na lekcji i to było tak, ale nie wiem skąd się to wzięło i jak dalej rozwiązać f(x)= a(x−3)(x−10) −8= a(4−3)(4−10) a=4/3

Janek191: Piszesz, ze nie miałaś funkcji kwadratowej, a f(x) = a*( x − 3)*( x − 10) , to funkcja kwadratowa w postaci iloczynowej

Mia: a umiesz to rozwiązać?

Eta: @Mia nie ma tu co rozwiązywać W zadaniu pytają o g(3) , g(10) , g(4) Sama już podałaś poprawne odpowiedzi w pierwszym poście 20: 23 Nie pytają jaki wzór ma funkcja f(x) i g(x)

5-latek: czyli mamy

	4
f(x)=		(x−3)(x−10)
	3

	4
f(x)=		x2−14x+40 taki jest wzor funkcji f(x) w postaci ogolnej (czyli postac iloczynowa
	3

zamieniłem na postac ogolna Funkcja g(x)=−f(x) (bo funkcje f(x) odbijamy wzglem osi OX

	4
Wiec funkcja g(x) ma postac g(x)= −		x2+14x−40
	3

	4
wiec g(3)= −		*32+14*3−40= policz
	3

Tak samo licz wartości tej funkcji dla pozostałych argumentow

Eta: f(3)=g(3)=0 i f(10)=g(10)=0 i f(4)= 8 ⇒ g(4)=−8 i to wszystko

5-latek: witam Teraz widze . dzięki To nabrałem sprawności rachunkowej

Janek191: