rownania wielomianowe ania: x²(2x−1)−162=0 czy mozna to rownanie rozwiazac inna metoda niz stosowanie twierdzenia o pierwiastkach wymiernych?

AS: Metody dokładne 1. Descartesa 2. Ferrariego 3. Eulera 4. Warmusa Przybliżone 1. metoda falsi 2. Newtona

Mila: Cardano.

Mariusz: 2x³−x²−162=0

	1		1
2(y+		)3−(y+		)2−162=0
	6		6

	1		1		1		1		1
2(y3+		y2+		y+		)−(y2+		y+		)−162=0
	2		12		216		3		36

	1		1		1		3
2y3+y2+		y+		−y2−		y−		−162=0
	6		108		3		108

	1		17494
2y3−		y+		=0
	6		108

	1		17494
y3−		y+		=0
	12		216

y=u+v

	1		17494
(u+v)3−		(u+v)+		=0
	12		216

	1		17494
u3+3u2v+3uv2+v3−		(u+v)+		=0
	12		216

	17494		1
u3+v3+		+3(u+v)(uv−		)=0
	216		36

	17494
u3+v3+		=0
	216

	1
(u+v)(uv−		)=0
	36

	17494
u3+v3=−
	216

	1
uv=
	36

	17494
u3+v3=−
	216

	1
u3v3=
	46656

	17494		1
t2+		t+		=0
	216		46656

	8747		76510008
(t+		)2−
	216		46656

	8747−√76510008		8747+√76510008
(t+		)(t+		)
	216		216

	1		1
y=		(−8747−√76510008)(1/3)+		(−8747+√76510008)(1/3)
	6		6

	1		1		1
x=		(−8747−√76510008)(1/3)+		(−8747+√76510008)(1/3)+
	6		6		6

Mila: 2x³−x²−162=0 162=1*2*81=1*2*9² W(1)≠0 W(−1)≠0 W(2)≠0 W(−2)≠0 W(9)≠0

	1
W(		)≠0
	2

	9		729		81		729		81
W(		)=2*		−		−162=		−		−162=0
	2		8		4		4		4

	9
x=
	2

Teraz schemat Hornera

ania: dziekuje pieknie

Mariusz: Tak Mila ale zastosowałaś(eś) to twierdzenie Zdaje się że ja pomyliłem znak , ale mimo to sposób dobry Możliwe że będzie trzeba skorzystać z zespolonych

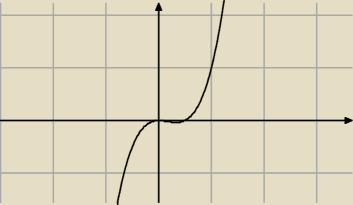PW: Każdy uczeń liceum powinien umieć narysować przybliżony przebieg funkcji h(x) = x²(2x−1).

	1
Wielomian h ma jeden pierwiastek podwójny x0=0 i drugi pierwiastek x1 =		.
	2

Myślę, że autor zadania specjalnie nie wymnożył x²(2x−1), żeby to zasugerować. Wykres występującej w zadaniu funkcji f(x) = h(x) − 162 powstaje w wyniku przesunięcia wykresu h o wektor [0, −162]. Wobec tego funkcja f ma jedno miejsce zerowe będące rozwiązaniem równania (1) x²(2x−1) = 162. Naturalną rzeczą jest sprawdzenie, czy szukane rozwiązanie nie jest liczbą naturalną. Sprawdzamy: − dla x = 4 jest 4²(2·4 −1) = 16·7 = 112 (liczba 4 jest za mała); − dla x = 5 jest 5²(2·5 −1) = 25·9 = 225 (liczba 5 jest za duża). Jest rzeczą oczywistą, że następne sprawdzenie wykonujemy dla leżącej w środku przedziału

	9
[4, 5] liczby		:
	2

	9		9		81
(		)2(2·		− 1) =		·8 = 162.
	2		2		4

Udało się − znaleźliśmy wymierny pierwiastek wielomianu f, a ponieważ innych pierwiastków nie ma, oznacza to koniec rozwiązania. Jest to moja odpowiedź na pytanie "czy można to równanie rozwiązać inną metodą". Wcale nie musieliśmy znać twierdzenia o wymiernych pierwiastkach wielomianu, żeby uzyskać poprawną odpowiedź.