Programowanie liniowe sese: Programowanie liniowe: Mam kilka warunków ograniczających, skąd wiadomo z którego warunku obliczam którą niewiadomą? np: f(x₁,x₂)=2x₁+3x₂ → max 2x₁+x₂≤20 x₁+x₂≤12 2x₁+2x₂≥16 x₁+3x₂≤30 x₁>0 x₂>0 i teraz z którego warunku obliczyć x₁ a z którego x₂?

sese: pomoże ktoś? bo tylko przez to robie źle całe zadania..

Dziadek Mróz: Simplex zna?

sese: nie

sese: i jak nie zna to jak?

sese: ?

sese: ogólnie całą metode graficzną taką jaką rozwiązuje znam. Tylko z tym mam problem co mam wyliczać z tych równań x1 czy x2 czy raz to raz to?

Dziadek Mróz: I jedno i drugie

sese: a skąd mam wiedzieć z którego równania którą wartość? Czy z każdego obydwie?

Dziadek Mróz: sese, chodzisz na wykłady i ćwiczenia?

sese: chodzę na wykłady może nie w 100% frekwencji, ale na ćwiczeniach jestem zawsze

Dziadek Mróz: No to chyba umiesz graficznie takie coś rozwiązać, nie? Rysujesz sobie proste dla każdego przypadku, później posuwasz się funkcją maksymalizacji i szukasz rozwiązań.

sese: umiem to robić. Nie rozumiesz mojego pytania. W tym przypadku mam 6 warunków ograniczających i z nich musze wyliczyć albo x1 albo x2. I nie wiem z którego warunku liczyć które, czy ze wszystkich np x1. Czy ze wszystkich x2? lub z któregoś x1 a z któregoś x2? jasne w tym przypadku do narysowania jest tylko równanie piąte i szóste, a te wcześniejsze musze wyznaczyć x1 i x2 i o to mi chodzi tylko

sese: Pomożesz?

Dziadek Mróz: 2x₁ + x₂ = 20 x₁ = 0 ⇒ x₂ = 20 x₂ = 0 ⇒ x₁ = 10 rysujesz prostą i tak dla reszty. Później rysujesz f dla wartości z wierzchołków zbioru i liczysz wartość tej f

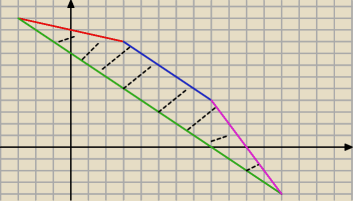
Dziadek Mróz: (max) f(x1, x2) = 2x₁ + 3x₂ 2x₁ + x₂ ≤ 20 x₁ + x₂ ≤ 12 2x₁ + 2x₂ ≥ 16 x₁ + 3x₂ ≤ 30 Mniej więcej taki rysunek wyjdzie

Dziadek Mróz: Z lekka już nie pamiętam dokładnie ale tak robiliśmy na zajęciach, że najpierw rysowaliśmy ograniczenia, a później dla wierzchołków obliczaliśmy funkcję i wyznaczaliśmy maksymalną wartość.

sese: a no i mi wychodzi tak samo dokładnie i to jest źle..

sese: tak najpierw ograniczenia potem gradient do gradientu prostopadle przchodzące przez charakterystyczne punkty i wybieram max albo min pkt. zalezy jaki mi potrzebny.

sese: tylko na zajęciach przekształacano każde równanie tak że odnosiło sie do jednej zmiennej np w tym wypadku było by tak chyba: x₂≤10−x₁ x₂>12−x₁ itd. i wtedy rysowaliśmy te ograniczenia

sese: albo nie umiem z tego odczytać poprawie maksimum... Jaki powinien być tutaj z tego obrazka pkt max? Bo mi wychodzi identyczny

sese: Udało się. Źle odczytywałem maksimum.... Dzięki wielkie Dziadek Mróz

Dziadek Mróz: maximum to (x₁, x₂) = (3, 9)