oblicz pole rombu ABCD, jeśli A(−2,−1), BC=[3,4], a wektor CD jest rownoległy do nanan: oblicz pole rombu ABCD, jeśli A(−2,−1), BC=[3,4], a wektor CD jest rownoległy do osi OX. Jak to zrobić z rysunkiem?

pigor: ..., otóż z warunków zadania, własności rombu i wektorów równoległych w rombie ABCD: jeśli A= (−2−1) i BC= [3,4}, to D= (−2+3,−1+4)= (1,3) i niech B=(x,−1), to C= (x+3,3), to wektory przekątnych AC= [x+3+2,3+1]= [x+5,4] i BD= [1−x,3+1]= [1−x,4] takie, że AC ⊥ BD ⇔ [x+5,4]◯[1−x,4]=0 ⇔ (x+5)(1−x)+4*4= 0 ⇔ ⇔ x−x²+5−5x+16= 0 ⇔ x²+4x−21= 0 ⇔ x= −7 v x=3, a więc są 2 takie przystające romby o polu powierzchni : P_ABCD= ¹₂|AC| * |BD|= ¹₂√ 8²+4² * √(−2)²+4², czyli P_ABCD= ¹₂*4√5*2√5= 4*5= 20 − szukane pole rombu . ...

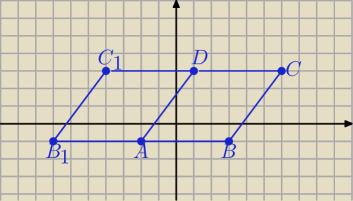
Eta: BC=AD=[3,4] ⇒ D(−2+3, −1+4)=(1,3) |BC|=|AB|= 5 i DC ∥ AB ∥OX ⇒ B(−2+5, −1)= (3, −1) lub B₁(−2−5, −1)=(−7,−1) Są dwa takie przystające romby AB=[5,0] AD=[3,4] to P= |5*4−3*0|= 20

Eta: Można jeszcze tak: |BC|= |AB|=a=5 A(−2, −1) , D(1,3) −− jak wyżej z treści zadania AB ⊂ y=−1 , DC⊂ y=3 to h= 4 i a=5 to P=a*h= 20