zagadnienia optymalizacyjne
Robert : Cześć wszystkim. Potrzebuje pomocy, mógłby ktoś mi rozpisać tak żeby było najprościej
wytłumaczone. ? Treść zadania: Jakie wymiary powinien mieć prostokąt o obwodzie równym 8, aby
walec, który powstanie z obrotu tego prostokąta dookoła jednego z boków miał:
a) największe pole powierzchni bocznej − to mam obliczone
b) największą objętość − przy tym nie mam kompletnie pomysłu .....

26 maj 21:09
irena_1:
H+r=4
H=4−r
0<r<4
V=πr
2(4−r)=π(−r
3+4r
2)
V'=π(−3r
2+8r)
V'=0
−r(3r−8)=0
r>0
27 maj 12:55
Przemysław: Spróbowałem trochę inaczej i coś nie wychodzi.
r
2πH=V
weźmy teraz trzy liczby: r,r,πH
średnia geometryczna:
3√rrπH=
3√V
| | 2r+πh | |
średnia arytmetyczna: |
| |
| | 3 | |
równość zachodzi tylko wtedy, gdy:
r=πH, więc wtedy objętość będzie maksymalna
z warunku r+H=4 mamy:
Ale ten mój wynik jest zły tylko nie wiem czemu

27 maj 13:26
Przemysław: W każdym razie można trochę inaczej:
r=4−H
(4−H)
2πH=V
liczby:
4−H,4−H,2H
G− śr geometryczna
A− śr arytmetyczna
3√2Vπ=G
G≤A
po przekształceniach:
równość dla 4−H=2H
| | 4 | | 4 | | 8 | |
czyli dla H= |
| , r=4− |
| = |
| |
| | 3 | | 3 | | 3 | |
27 maj 14:32
Robert :
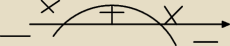
w punkcie b proszą o największa objętość, kończąc Ireny początek, miejsca zerowe 8xπ−3a
2π to
x=1 i x= 8/3
27 maj 19:20
J:
a skąd miejsce zerowe: x = 1
27 maj 19:22
Robert :
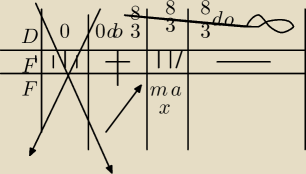
do wzoru F(x) podstawiamy 8/3 i wychodzi 256/27 π, ktoś może kojarzy albo sprawdzi poprawność
za F(8/3) = 4x
2π −x
3π za x inaczej r, wstawiłem 8/3 co myślicie ? o tym
27 maj 19:30
Robert : przepraszam x= 0 i x= 8/3
27 maj 19:30
Robert : mo 8xπ− 3x2π= 0 więc x(8π−3xπ)= 0 i rozwiązania 0 i 8/3
27 maj 19:32
J:
ja myślę,że dalej nie masz pojęcia o co chodzi w tym zadaniu
27 maj 19:37
Robert :
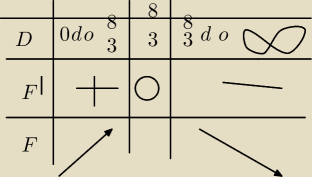
poprawiona tabelka, co dalej ? czy o to chodzi, do tego momentu rozumiem
27 maj 19:46
J:
| | 8 | |
chcesz sprawdzić, czy w punkcie: r = |
| funkcja osiaga maksimum ? |
| | 3 | |
27 maj 19:51
Robert : ta wartość co wyjdzie w MAX to będzie wartością max objętości ? tak ?
27 maj 20:00
J:
| | 8 | |
człowieku, co Ty mącisz ? funkcja osiąga maksimum dla r = |
| |
| | 3 | |
| | 8 | | 8 | |
czyli maksymalna objętośćm jest dla: r = |
| i H = 4 − |
| |
| | 3 | | 3 | |
27 maj 20:07
Robert : i wtedy podstawić pod wzór na objętość ? co dalej ? czy to wszystko ?
27 maj 20:13
Przemysław: Jeżeli chcesz znać maksymalną objętość to tak,
| | 8 | | 4 | |
ale pytanie było o wymiary, a wymiary znasz: r= |
| , H= |
| . |
| | 3 | | 3 | |
27 maj 20:22
Robert : Dziękuje za pomoc bardzo ! faktycznie później sobie komplikowałem sam, ale już wiem o co chodzi

27 maj 20:24
Przemysław: Spoko.
Pytanie kontrolne: po co Ci tu pochodna?

27 maj 20:25
Robert : w pkt. A) pochodną liczyłem mo pochodnej szkic i tabelke i w ten sposób po przekształceniu
wzoru na Pole boczne obliczyłem a i b i obliczyłem Pole boczne. Taką chciałeś odpowiedź jesli
nie, to proszę wytłumacz
27 maj 20:42
Przemysław: Sorki, dopiero zobaczyłem

Chodziło mi o to, że pochodna mówi Ci jak zmienia się funkcja (rośnie, maleje, jest stała).
Jeżeli pochodna jest zerowa w danym punkcie to możemy podejrzewać, że funkcja badana ma tam
ekstremum (jeżeli pochodna w tym punkcie zmienia znak).
Dlatego można przyrównać pochodną do zera. Dostaniemy punkty (jeden odrzucamy, bo r jest
długością boka prostokąta, więc cięzko, żeby było to zero). Patrzymy na wykres pochodnej.
| | 8 | |
W tym punkcie, który nam został (r= |
| ) pochodna zmienia znak, z "+" na "−". |
| | 3 | |
Czyli funkcja rosła zanim dotarła do punktu, gdzie pochodna się zeruje. Za tym punktem maleje.
Czyli musiała osiągnąć jakieś maksimum. I to maksimum jest dokładnie w punkcie, gdzie funkcja
się zatrzymała (pochodna była zero). Dlatego dla tego wyliczonego r, objętość (nasza badana
funkcja) przyjmuje swoje maksimum. Długość drugiego boku (H) otrzymujemy z danych o obwodzie.
Jak zawsze mam nadzieję, że nie pomyliłem się i nie napisałem głupot

27 maj 21:35
Robert : Po przeczytaniu twojej wypowiedzi, zgadzam się z tobą, odpowiedź jak najbardziej zrozumiała.
Cieszy mnie to że są jeszcze tacy ludzi co pomagają bezinteresownie. Dzięki /sup>^
27 maj 22:17
Przemysław: Spoko

Dodatkowo można też się bawić tak jak ja tam robiłem z nierównością między średnimi
(post z 14:32), ale tak chyba jest ciężej (i nie wiem, czy dobrze to zrobiłem).
27 maj 22:36
Robert : Nie za bardzo rozumiem tych średnich, tego rozwiązania z godz 14"32
27 maj 22:48
Przemysław: r
2*π*H=V
r=H−4, bo r+H=4
(4−H)
2πH=V
teraz biorę liczby:
4−H,4−H,2H
I jest prawdziwe, dla każdych liczb (a więc w szczególności dla tych, które dobrałem), że ich
średnia geometryczna jest ≤ ich średniej arytmetycznej.
Dodatkowo równość zachodzi tylko, gdy wszystkie liczby są sobie równe.
więc liczę średnią geometryczną, nazwę ją G:
G=
3√(4−H)2*2H
zauważmy że G=
3√2Vπ <−− możesz sobie wstawić V i powinno wyjść, że to prawda
liczę teraz średnią geometryczną, nazwę ją A:
Mamy więc z tego faktu o nierówności:
G≤A
objętość jest
najwyżej równa wyrażeniu po prawej stronie
a równość ta zachodzi, gdy wszystkie liczby (z naszych dobranych) są równe
4−H=4−H jest oczywiste
teraz ma być jeszcze:
4−H=2H
4=3H
Ale mówię, nie jestem pewien czy to jest dobrze

(znaczy wynik ok, ale nie wiem, czy
rozumowanie jest całkiem ok)
27 maj 22:57


 w punkcie b proszą o największa objętość, kończąc Ireny początek, miejsca zerowe 8xπ−3a2π to
x=1 i x= 8/3
w punkcie b proszą o największa objętość, kończąc Ireny początek, miejsca zerowe 8xπ−3a2π to
x=1 i x= 8/3
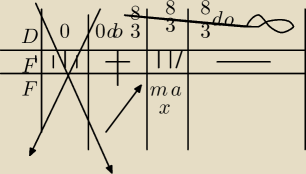 do wzoru F(x) podstawiamy 8/3 i wychodzi 256/27 π, ktoś może kojarzy albo sprawdzi poprawność
za F(8/3) = 4x2π −x3π za x inaczej r, wstawiłem 8/3 co myślicie ? o tym
do wzoru F(x) podstawiamy 8/3 i wychodzi 256/27 π, ktoś może kojarzy albo sprawdzi poprawność
za F(8/3) = 4x2π −x3π za x inaczej r, wstawiłem 8/3 co myślicie ? o tym
 poprawiona tabelka, co dalej ? czy o to chodzi, do tego momentu rozumiem
poprawiona tabelka, co dalej ? czy o to chodzi, do tego momentu rozumiem


 Chodziło mi o to, że pochodna mówi Ci jak zmienia się funkcja (rośnie, maleje, jest stała).
Jeżeli pochodna jest zerowa w danym punkcie to możemy podejrzewać, że funkcja badana ma tam
ekstremum (jeżeli pochodna w tym punkcie zmienia znak).
Dlatego można przyrównać pochodną do zera. Dostaniemy punkty (jeden odrzucamy, bo r jest
długością boka prostokąta, więc cięzko, żeby było to zero). Patrzymy na wykres pochodnej.
Chodziło mi o to, że pochodna mówi Ci jak zmienia się funkcja (rośnie, maleje, jest stała).
Jeżeli pochodna jest zerowa w danym punkcie to możemy podejrzewać, że funkcja badana ma tam
ekstremum (jeżeli pochodna w tym punkcie zmienia znak).
Dlatego można przyrównać pochodną do zera. Dostaniemy punkty (jeden odrzucamy, bo r jest
długością boka prostokąta, więc cięzko, żeby było to zero). Patrzymy na wykres pochodnej.

 Dodatkowo można też się bawić tak jak ja tam robiłem z nierównością między średnimi
(post z 14:32), ale tak chyba jest ciężej (i nie wiem, czy dobrze to zrobiłem).
Dodatkowo można też się bawić tak jak ja tam robiłem z nierównością między średnimi
(post z 14:32), ale tak chyba jest ciężej (i nie wiem, czy dobrze to zrobiłem).
 (znaczy wynik ok, ale nie wiem, czy
rozumowanie jest całkiem ok)
(znaczy wynik ok, ale nie wiem, czy
rozumowanie jest całkiem ok)