Geometria analityczna (początki) Filip: Trójkąt ABC jest równoramienny, w którym AC=BC. Podstawa AB zawiera się w prostej k: 3x−7y+35=0, zaś ramię BC zawiera się w prostej l: 5x−2y−19=0. Wyznacz równanie prostej ,w której zawiera się bok AC tego trójkąta, jeśli wiadomo, że punkt P(−2,0 )należy do boku AC. Po rozrysowaniu dwóch prostych nie wiem co dalej zrobić Proszę o pomoc

Mila: Jeśli masz odpowiedź, to napisz. Rozwiązuję.

Filip: @Mila Momencik, aby wrócę do domu. Z góry dziękuję za samą fatygę.

Filip: 2x+5y+4=0

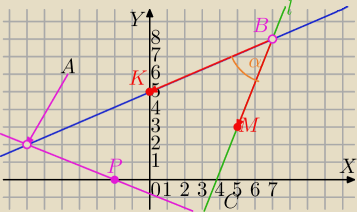
Mila: k: 3x−7y+35=0 3x+35=7y

	3
y=		x+5
	7

l: 5x−2y−19=0 5x−19=2y

	5		19
l: y=		x−
	2		2

3		5		19
	x+5=		x−
7		2		2

x=7 y=8 B=(7,8) Obieram punkty: K∊k, M∊l K=(0,5)∊k M=(5,3)∊l BK^→=[−7,−3], |BK|=√49+9=√58 BM^→=[−2,−5], |BM|=√4+25=√29 Obliczam kąt między prostymi k i l ( można z wzoru, ja liczę z iloczynu skalarnego wektorów) BK^→ o BM^→=(−7)*(−2)+(−3)*(−5)=14+15=29 BK^→ o BM^→=|BK|*|BM|*cosα 29=√58*√29*cosα

	29		29		√2
cosα=		=		=		⇔
	√2*29*√29		29*√2		2

α=45⁰ ∡A=∡B=45^o⇔∡C=90^o⇔ Prosta AC⊥l i P∊AC AC: y=ax+b

	2
a=−
	5

	2
0=−		*(−2)+b
	5

	4
b=−
	5

AC:

	2		4
y=−		x−
	5		5

==================

Mila: Kąt między prostymi w postaci kierunkowej:

	|a1−a2|
tgα=
	1+a1*a2

	3   5   | − |   7   2		6   35   | − |   14   14
tgα=		=		=
	3   5   1+ *   7   2		15   1+   14

	29   14
tgα=		=1
	29   14

α=45^o

Filip: @Mila Jestem wdzięczny za poświęcony czas i zadanie Cieszę się, że są takie osoby

Mila: Teraz analizuj, trochę podstępne to zadanie.

pigor: ..., . Trójkąt ABC jest równoramienny, w którym AC=BC. Podstawa AB zawiera się w prostej k : 3x−7y+35=0, zaś ramię BC w prostej l : 5x−2y−19=0. Wyznacz równanie prostej w której zawiera się bok AC tego trójkąta, jeśli wiadomo, że punkt P=(−2,0 )należy do boku AC −−−−−−−−−−−−−−−−−−−−−−−−−− no to do szuflady mojej Mai np. tak ; niech β miara kąta przy podstawie danego Δ, czyli między AB i BC, to

	[3,−7] ◯[5,−2]		15+14
cosβ=		=		=
	√9+49 *√25+4		√58* √29

	29		1
=		=		⇒ β=45o , więc ΔABC − prostokątny
	√2*29* √29		√2

równoramienny, a wektor normalny prostej BC to [5,−2] − jednocześnie

	x+2		y−0
kierunkowy prostej AC, czyli AC :		=		⇔ −2x−4 = 5y ⇔
	5		−2

⇔ 2x+5y+4=0 − szukane równanie prostej zawierającej bok AC....